c++ でカルマンフィルタを実装する with バネ・マス・ダンパ系

Control

カルマンフィルタの以下の本に例題として matlab によるカルマンフィルタの実装がなされていました。自分の理解を深めるためにも、c++ で実装してみようと思い、本記事を書いています。

カルマンフィルタの基本的な数式

システムの離散時間状態方程式は以下のように与えられているものとします。

\begin{align}
x (k+1) &= A x (k) + B u (k) + B_v v (k) \\
y (k) &= C x (k) + w(k)
\end{align}

上記システムで、変数はそれぞれ以下を表しています。

$x(k)$システムの状態
$u(k)$システムの入力
$y(k)$システムの出力
$v(k)$システム雑音
$w(k)$観測雑音

ここで、システム雑音 $v(k)$ の共分散行列を $Q$、観測雑音 $w(k)$ の共分散行列を $R$ と定義します。これらの雑音は、平均値 $0$ の正規性白色雑音であると仮定します。

カルマンフィルタは、以下の2ステップで状態を逐次的に推定していきます。

予測ステップ

\begin{align}
事前状態推定値&: \hat{x} ^- (k) = A \hat{x} (k-1) + B u (k-1) \\
事前誤差共分散行列&: P^- (k) = A P (k-1) A^T + B_v Q B_v^T
\end{align}

フィルタリングステップ

\begin{align}
カルマンゲイン行列&: G (k) = P^- (k) C^T (C P(k)^- C^T + R)^{-1} \\
状態推定値&: \hat{x} (k) = \hat{x}^-(k) + G (k)(y (k) \ – \ C \hat{x}^- (k)) \\
事後誤差共分散行列&: P(k) = (I \ – \ G(k) C) P^- (k)
\end{align}

詳細は、「カルマンフィルタの基礎 6.5節 システム制御のためのカルマンフィルタ」をご参照ください。

※多変数を取り扱う形式に一般化したかったため、変数名が参考書籍と若干異なることにご注意ください。「Point 6.7 多変数時系列データに対するカルマンフィルタ」も参考にしています。

例題

モデル

Fig 1: Spring-Mass-Damper system

バネ・マス・ダンパ系を考えます。qiita の記事を参考にしました。カートがバネで壁から繋がれているモデルです。簡単のため、地面と車輪の摩擦は考慮しません。

バネの自然長からの変位を $\xi(t)$、カートに加えられる力を $f(t)$ として、以下のように物理パラメータを定義したとき

$m$カートの質量
$k$バネ定数
$c$減衰係数

バネ・マス・ダンパ系の運動方程式は、以下のようになります。

\begin{align}
m \ddot{\xi}(t) + c \dot{\xi}(t) + k \xi(t) = f(t)
\end{align}

状態方程式

状態 $x$ を変位と速度のベクトル $x = [\xi (t), \ \dot \xi (t)]^T$、入力 $u = f(t)$ をカートに加えられる力、出力 $y = \xi(t)$ をカートの変位として、システムの状態方程式を以下のように表現します。

\begin{align}
\dot x &= A x + B u \tag{1} \label{continuous_system} \\
y &= C x + D u
\end{align}

ただし、システム行列 $A, B, C, D$ をそれぞれ以下のように定めます。

\begin{align}
A =
\begin{bmatrix}
0 & 1 \\
-\frac{k}{m} & -\frac{c}{m}
\end{bmatrix}, \
B =
\begin{bmatrix}
0 \\ \frac{1}{m}
\end{bmatrix} , \
C =
\begin{bmatrix}
1 & 0
\end{bmatrix}, \
D = 0 \tag{2} \label{continuous_system_matrix}
\end{align}

今回は簡単のため、$m = k = c = 1$ のケースを考えます。

離散化

最後にシステムの離散化表現を考えます。状態方程式の離散化に関しては、この動画を参考にしました。

(1) を離散化した状態方程式は、以下のようになります。

\begin{align}
x(k+1) &= A_d x(k) + B_d u(k) \\
y(k) &= C_d x(k) + D_d u(k)
\end{align}

ここで、$A_d, \ B_d, \ C_d, \ D_d$ はそれぞれ以下を満たします。

\begin{align}
A_d = (I + A \Delta t), \
B_d = B \Delta t, \
C_d = C, \
D_d = D
\end{align}

今回は、$\Delta t = 0.01$ すなわちサンプリング周期を $10 \, \text{ms} \, (0.01 \, \text{s})$ とします。

$(2)$ と $m = k = c = 1$ より、離散化された状態方程式のシステム行列は最終的に以下のように記述できます。

\begin{align}
A_d =
\begin{bmatrix}
1 & 0.01 \\
-0.01 & 0.99
\end{bmatrix}, \
B_d =
\begin{bmatrix}
0 \\ 0.01
\end{bmatrix} , \
C_d =
\begin{bmatrix}
1 & 0
\end{bmatrix}, \
D_d = 0
\end{align}

さらに、システム雑音 $v(k)$・観測雑音 $w(k)$ も考慮すると、離散化された状態方程式は最終的に以下のようになります。

\begin{align}
x(k+1) &= A_d x(k) + B_d u(k) + B_d v(k) \\
y(k) &= C_d x(k) + D_d u(k) + w(k)
\end{align}

ソースコード

ソースコードは github に載せているので、詳しくはこちらをご確認ください。ドキュメントも doxygen により生成しています。

準備

Eigen library

行列演算のため、Eigen ライブラリを PC にダウンロードする必要があります。

Linux / Mac の場合は、ライブラリをコチラからダウンロードしてきて Eigen ディレクトリを /usr/local/include/ に置けば大丈夫です。

On Linux or Mac OS X, another option is to symlink or copy the Eigen folder into /usr/local/include/.

Eigen: Getting started

gnuplot

グラフを出力するために gnuplot が必要です。ubuntu であれば以下のコマンドで簡単にインストールできます。

sudo apt-get install gnuplot

カルマンフィルタの実装

フィルタリングのプロセスのソースコードを貼り付けておきます。他の部分は github をご参照ください。

Eigen::VectorXf KalmanFilter::filter(const Eigen::VectorXf& pre_x_hat,
                                     const Eigen::VectorXf& pre_u,
                                     const Eigen::VectorXf& cur_y) {
  if (!check_filter_matrix_vector_size(pre_x_hat, pre_u, cur_y))
    return pre_x_hat;

  /// prediction step
  Eigen::VectorXf x_hat_ps = A_ * pre_x_hat + B_ * pre_u;
  Eigen::MatrixXf P_ps = A_ * P_ * A_.transpose() + Bv_ * Q_ * Bv_.transpose();

  /// filtering step
  Eigen::MatrixXf G =
      P_ps * C_.transpose() * (C_ * P_ps * C_.transpose() + R_).inverse();
  Eigen::VectorXf new_x_hat = x_hat_ps + G * (cur_y - C_ * x_hat_ps);
  Eigen::MatrixXf I = Eigen::MatrixXf::Identity(A_.cols(), A_.cols());
  P_ = (I - G * C_) * P_ps;

  return new_x_hat;
}

バネ・マス・ダンパ系の例題

こちらも乱数の生成やグラフプロット用のファイル保存に関するソースコードは省きます。大まかな流れは、以下のようになります。

  1. 物理パラメータ・システム行列の定義：initialize()
  2. 観測値・真値を計算：simulate_dynamics()
  3. カルマンフィルタで状態推定：estimate_states()

initialize()

void SpringMassDamper::initialize() {
  /// physical parameter
  float m = 1.0;
  float k = 1.0;
  float c = 1.0;

  /// system matrices
  Eigen::MatrixXf A(2, 2);
  A << 0.0, 1.0, -k / m, -c / m;
  Eigen::MatrixXf Ad(2, 2);
  Ad = Eigen::MatrixXf::Identity(2, 2) + A * delta_t_;

  Eigen::MatrixXf B(2, 1);
  B << 0, 1 / m;
  Eigen::MatrixXf Bd(2, 1);
  Bd = B * delta_t_;

  Eigen::MatrixXf Cd(1, 2);
  Cd << 1.0, 0.0;

  Eigen::MatrixXf Dd(1, 1);
  Dd << 0.0;

  /// covariance matrices
  float gamma = 0.0;
  Eigen::Matrix2f P0 = gamma * Eigen::Matrix2f::Identity();

  float sigma_v = 1e-2;
  Eigen::MatrixXf Q(1, 1);  // sigma_v^2
  Q << sigma_v * sigma_v;

  float sigma_w = 5.0 * 1e-3;
  // float sigma_w = 5.0 * 1e-6;
  Eigen::MatrixXf R(1, 1);  // sigma_w^2
  R << sigma_w * sigma_w;

  kf_ = std::make_shared<KalmanFilter>(P0, Ad, Bd, Bd, Cd, Dd, Q, R);
  simulate_dynamics(Ad, Bd, Cd, Dd);
}

simulate_dynamics()

void SpringMassDamper::simulate_dynamics(const Eigen::MatrixXf& Ad,
                                         const Eigen::MatrixXf& Bd,
                                         const Eigen::MatrixXf& Cd,
                                         const Eigen::MatrixXf& Dd) {
  /// parameter for noise and input
  float sigma_v = 1e-2;
  float sigma_w = 5.0 * 1e-3;
  float u_rand_max = 0.5;

  /// generate random numbers for v and w
  int rand_size = sim_times_ + 1;
  std::vector<float> rand_nd_v = generate_rand_nd(rand_size);
  std::vector<float> rand_nd_w = generate_rand_nd(rand_size);

	/// initialize setting for random number u
  std::srand(2);

  // define 1-dimentional vector as follows
  Eigen::Matrix<float, 1, 1> v(sigma_v * rand_nd_v[0]);
  Eigen::Matrix<float, 1, 1> w(sigma_w * rand_nd_w[0]);

  Eigen::Vector2f x(0, 0);
  Eigen::Matrix<float, 1, 1> u(u_rand_max * get_rand_m1p1());
  Eigen::Matrix<float, 1, 1> y = Cd * x + Dd * u + w;
  x_v_.push_back(x);
  u_v_.push_back(u);
  y_v_.push_back(y);

  for (int i = 0; i < sim_times_; i++) {
    /// generate noise
    v(0, 0) = sigma_v * rand_nd_v[i + 1];
    w(0, 0) = sigma_w * rand_nd_w[i + 1];

    /// generate input
    u(0, 0) = u_rand_max * get_rand_m1p1();

    /// calculate states
    x = Ad * x + Bd * u + Bd * v;
    y = Cd * x + Dd * u + w;

    x_v_.push_back(x);
    y_v_.push_back(y);
    u_v_.push_back(u);
  }
}

estimate_states()

void SpringMassDamper::estimate_states() {
  Eigen::Vector2f x_hat(0, 0);
  x_hat_v_.push_back(x_hat);

  /// calculate filtered value
  for (int i = 1; i < sim_times_; i++) {
    x_hat = kf_->filter(x_hat, u_v_[i - 1], y_v_[i]);
    x_hat_v_.push_back(x_hat);
  }
}

参考

  • doxygen
    • 書き方をわかりやすく解説している Qiita 記事（参考）
    • Doxyfile の例（参考）
    • private 関数もドキュメントに含める（参考）
  • Eigen ライブラリ
    • 1次元の Vector を定義するための方法（参考）
  • c++ で正規分布に従った乱数の生成（参考）
  • c++ と gnuplot でデータをプロットする（参考）
  • ユニットテスト
    • テストコードで、private メンバにアクセスする（参考）

シミュレーション

設定

初期状態や物理パラメータを以下のように定めて、シミュレーションを行います。

初期状態$(x, \dot x)$$(0, 0)$$(\mathrm{m}, \mathrm{m/s})$
初期推定値$(\hat x, \dot{\hat x})$$(0, 0)$$(\mathrm{m}, \mathrm{m/s})$
共分散行列の初期値$P_0$$\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$
質量$m$$1.0$$\mathrm{kg}$
バネ定数$k$$1.0$$\mathrm{N/m}$
減衰係数$c$$1.0$$\mathrm{Ns/m}$
システム雑音の標準偏差$\sigma_v$$1.0 \times 10^{-2}$$\mathrm{N}$
観測雑音の標準偏差$\sigma_w$$5.0 \times 10^{-3}$$\mathrm{m}$
制御入力乱数の最大値$u_{max}$$0.5$$\mathrm{N}$
シミュレーション間隔$\Delta t$$0.01$$\mathrm{s}$
シミュレーション時間$T$$10.0$$\mathrm{s}$

カルマンフィルタの共分散行列の初期値 $P_0$ は、$\gamma$ を $0 \, \text{〜} \, 1000$ の値、$I$ を単位行列として、以下のように定めることが一般的です。SN 比が悪い場合は $\gamma$ を小さくした方が良いそうです。（「カルマンフィルタの基礎 6.3.5節」参考）

\begin{align}
P_0 = \gamma I
\end{align}

今回は $\gamma = 0$ と設定しました。

システム雑音 $v$、観測雑音 $w$ は、標準偏差がそれぞれ $\sigma_v, \sigma_w$ となるような正規分布に従う乱数とします。たとえば、システム雑音の標準偏差は $1.0 \times 10^{-2}$ と設定しています。これは、指令した制御入力と実際の入力の間の誤差が約 $68 \, \text{%}$ の確率で $\pm 0.01 \, \mathrm{N}$ 以内に収まることを意味しています。

※カルマンフィルタは正規性白色雑音で駆動されるシステムを仮定しますが、このシミュレーション例だと白色性は保証できていないです。

制御入力 $u$ は、以下を満たす c++ の rand() 関数で生成されるランダムな値とします。

\begin{align}
-u_{max} \, \leq \, u \, \leq \, u_{max}
\end{align}

結果

共分散行列 $Q, R$ が実際の雑音の分散と同じ場合

カルマンフィルタの予測ステップ・フィルタリングステップで使われる $Q, R$ が以下を満たす場合を考えます。

\begin{align}
Q &= \sigma_v^2 = 1.0 \times 10^{-4} \\
R &= \sigma_w^2 = 2.5 \times 10^{-5}
\end{align}

これは、カルマンフィルタを適用する段階で予め雑音の分散が既知であることを意味します。

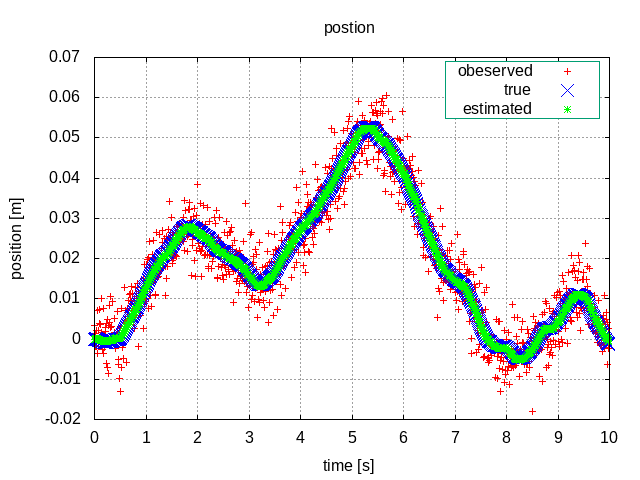
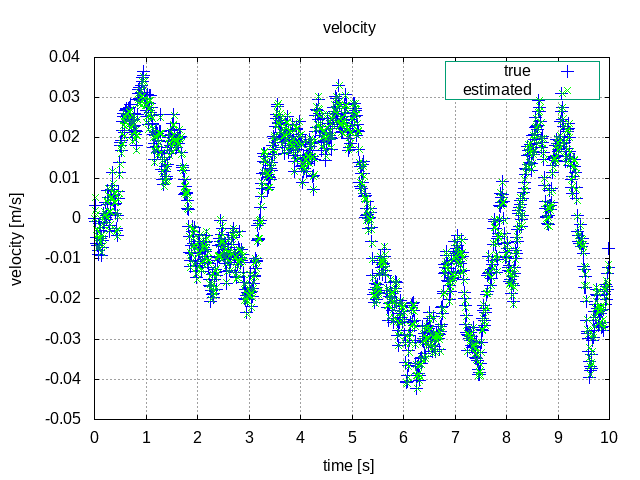
観測雑音が入ったデータの観測値、システム雑音のみが入った真値、カルマンフィルタによる推定値、ランダムな制御入力をそれぞれ図示します。

位置

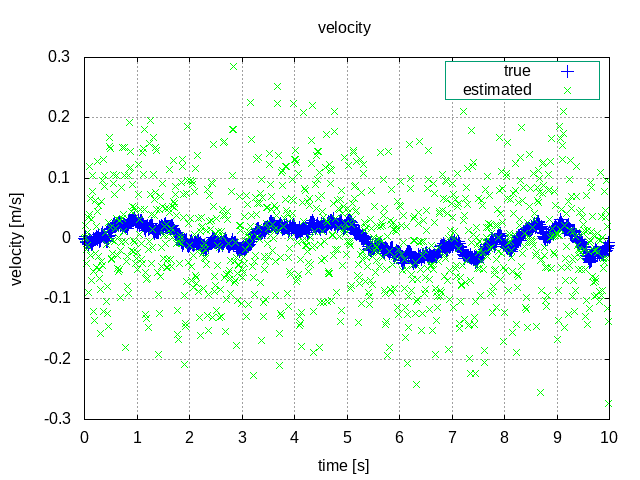
速度

入力

観測値にはかなりノイズが乗っているものの、位置・速度の推定値ともに真値とかなり近い値になっていることがわかります。

共分散行列 $Q, R$ が実際の雑音の分散と異なる場合

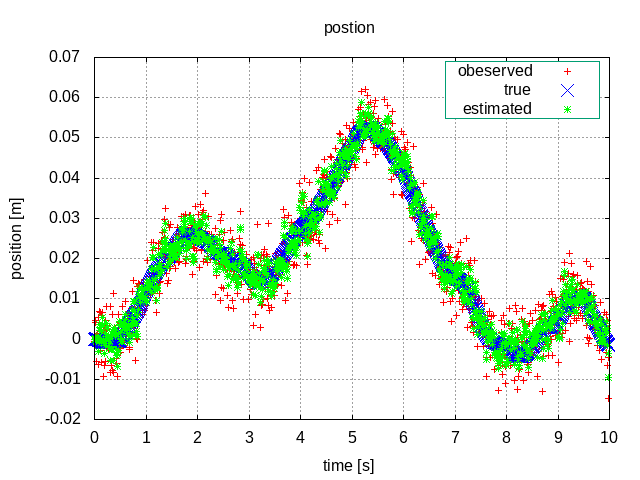
以下のように、カルマンフィルタで使用する共分散行列と実際の雑音の分散に差異がある場合を考えます。

\begin{align}
Q &= 1.0 \times 10^{-4} = (1.0 \times 10^{-2})^2 \\
R &= 2.5 \times 10^{-11} = (5.0 \times 10^{-6})^2
\end{align}

このとき、カルマンフィルタ側では観測値の誤差の標準偏差が $5.0 \times 10^{^-6}$ であると仮定しています。これは、実際よりも観測誤差は少ないものとして（実際よりも観測値を過剰に信用して）状態推定を行っていることを意味します。

グラフからもわかる通り、真値と推定値は大幅にずれてしまっていることがわかります。特に、速度はほぼ推定できていないです。

位置

速度

定量的な評価

以下のようなプログラムで、位置の推定値と真値の誤差の積算値を算出してみました。

  float total_error = 0.0;
  for (int i=0; i<smd.sim_times_; i++) {
    total_error += std::fabs(smd.x_hat_v_[i](0) - smd.x_v_[i](0));
  }

「共分散行列 $Q, R$ が実際の雑音の分散と同じ場合」は $0.436987$ となり、「共分散行列 $Q, R$ が実際の雑音の分散と異なる場合」は $2.54736$ となっていました。

定量的な評価からも、カルマンフィルタに設定する $Q, R$ 共分散行列は非常に重要なパラメータであることがわかります。

まとめ

今回は、c++ でカルマンフィルタの実装をして、バネ・マス・ダンパ系の例を通してカルマンフィルタの効果を検証してみました。観測誤差があっても共分散行列が正しく設定されていれば、正確に状態推定できることを確認できました。

コメント