運動方程式導出の記事に引き続き、シミュレーションを行っていきます。本記事は、物理パラメータの選定・制御則構築・数値シミュレーション等について解説していきます。
はじめに
前回と同様、今回もソースコードはこちらを参照していただければと思います。ソースコード上のタイトルと下記の目次が対応するようになっているます。たとえば、最初の節は physical parameter substitution というタイトルの箇所をソースコード上で探せば該当するコードを読めます。
簡易的なシミュレーションの方法と LQR コントローラ構築方法については、以下の Qiita の記事を参考にしました。
二輪ロボットの数値シミュレーションを sympy ベースで行っている以下の記事も参考にしました。
物理パラメータ(physical parameter substitution)
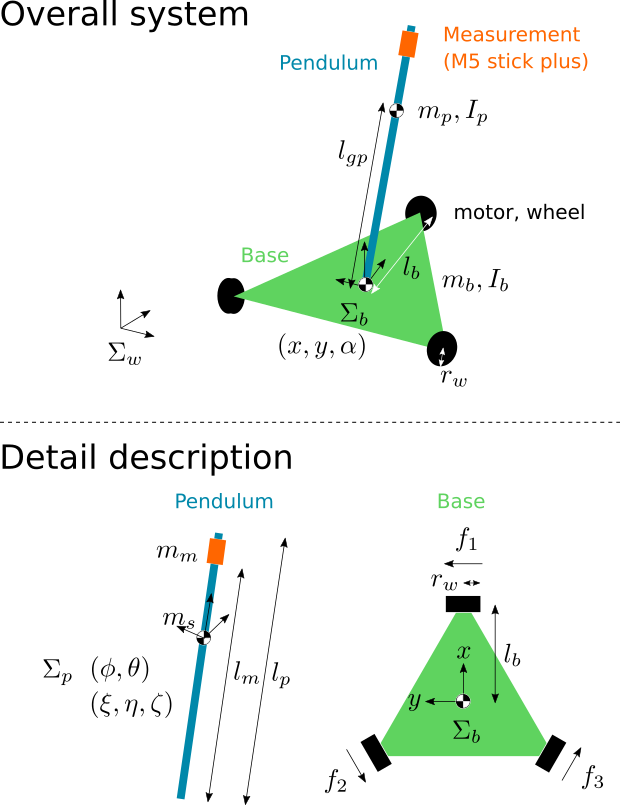
左図と右表のパラメータが対応しています。物理パラメータについての詳細は、前回の記事を読んでいただければと思います。
| 変数名 | 値 | 単位 |
| $g$ | 9.8 | $\mathrm{m/s^2}$ |
| $m_b$ | 0.5 | $\mathrm{kg}$ |
| $l_b$ | 0.12 | $\mathrm{m}$ |
| $r_w$ | 0.03 | $\mathrm{m}$ |
| $I_{bzz}$ | 0.0018 | $\mathrm{kg \cdot m^2}$ |
| $m_p$ | 0.01 | $\mathrm{kg}$ |
| $l_p$ | 2.0 | $\mathrm{m}$ |
| $\pi$ | 3.14 |
実際にロボットはまだ作っていないので、パラメータの値は結構テキトーです。
振子の長さはある程度長くしておかないと安定化できないと思うので、$l_p = 2.0 \mathrm{m}$ としています。
$I_{bzz}$ はこのサイトに記載されていた三角形の慣性モーメントの求め方を参考にし、$I_{bzz} = 0.0018$ と割り出しました。正三角形の重心周りの慣性モーメント $I_z$ は、一辺の長さを $a$ としたとき、以下のように求まります。
$$ I_{z} = \frac{1}{12} m a^2 $$
上記の物理パラメータを代入して、非線形システムの関数 f_sim と線形システムの $A, B$ 行列 A_sim, B_sim を求めています。A_sim, B_sim を求める際、データ型を np.float64 としておかないと、あとでリカッチ方程式を解くときにエラーが発生してしまいます(参考サイト)。
非線形システム(nonlinear system)
数値シミュレーションを行うために、現在の状態 $x$ と入力 $u$ から $\dot x$ を出力する関数 nonlinear_model() を定義しました。戻り値は numpy の配列にしています。msubs の使い方に関してはこのサイトを参考にしました。
LQR コントローラ(LQR controller)
今回のシミュレーションでは、LQR コントローラを設計して使用します。scipy にはリカッチ方程式を解いて LQR コントローラの係数ベクトルを算出するライブラリがあるようなので、これを使いました。
P = linalg.solve_continuous_are(A_sim, B_sim, Q, R)
K = linalg.inv(R).dot(B_sim.T).dot(P)
E = linalg.eigvals(A_sim - B_sim.dot(K))$Q$ も $R$ も単位行列とした場合、システムを安定化できませんでした。おそらく加えている入力が大きすぎることが原因だったので、入力の重みを大きくして、あまり入力を使わないような制御則を設計したところ、後続のシミュレーションでシステムの安定化が達成されました。
具体的には、以下のように $Q, R$ 行列を定めました。
\begin{align}
Q &= I_{10} \\
R &= 10 \times I_{3}
\end{align}
ここで、$I_{n}$ を $n \times n$ の大きさの単位行列としています。
上記のコードによって設計されたコントローラは $K$ です。
数値シミュレーション(execute simulation)
上述の物理パラメータや制御則を使って、実際にシミュレーションを行っていきます。シミュレーションの設定は下記のようにしました。
| 変数名 | 内容 | 値 | 単位 |
| $T$ | シミュレーション時間 | 20 | $\mathrm{s}$ |
| $dt$ | シミュレーション間隔 | 0.02 | $\mathrm{s}$ |
| $\phi_0$ | $\phi$ の初期角度 | 0.1 | $\mathrm{rad}$ |
| $\theta_0$ | $\theta$ の初期角度 | -0.1 | $\mathrm{rad}$ |
シミュレーション間隔は、制御周期が $20 \, \mathrm{ms}$ くらいであることを想定して、同じくらいの値にしました。
振子の初期角度 $\phi_0$ と $\theta_0$ をそれぞれ
\begin{align}
\phi_0 &= 0.1 \, \mathrm{rad} \fallingdotseq 5.73 \, \mathrm{deg} \\
\theta_0 &= -0.1 \, \mathrm{rad} \fallingdotseq -5.73 \, \mathrm{deg}
\end{align}
とします。その他の状態・入力の初期値はそれぞれ 0 としています。
for i in range(1, len(t_sim)):
u_sim[i] = -np.dot(K, x_sim[i-1,:])
dx_sim = nonlinear_model(x_sim[i-1,:], u_sim[i,:])
x_sim[i,:] = x_sim[i-1,:] + dx_sim * dt_sim上記のコードでは、以下のステップで逐次的に状態ベクトルを求めています。
- 前回の状態 $x(k-1)$ から現在の入力 $u(k)$ を計算する。
$ u(k) = -K x(k-1) $ - 今回の入力 $u(k)$ と前回の状態 $x(k-1)$ から、現在の状態の時間微分 $\dot{x} (k)$ を計算する。
$ \dot{x} (k) = f(x(k-1), \, u(k))$ - 前回の状態 $x(k-1)$ と現在の状態の時間微分 $\dot{x} (k)$ から、現在の状態 $x(k)$ を求める。
$ x(k) = x(k-1) + \dot{x} (t) dt $
グラフ描画(plot figures)
上記の設定でシミュレーションを行った結果を、以下のグラフに描画します。
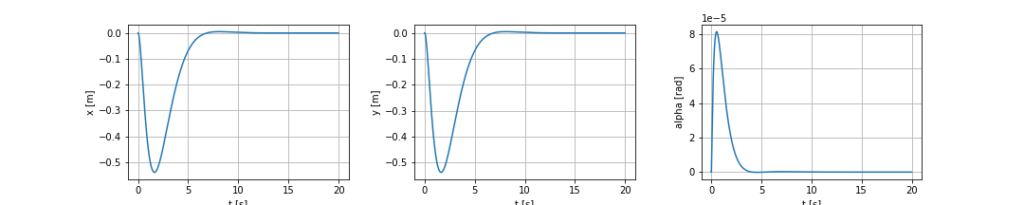
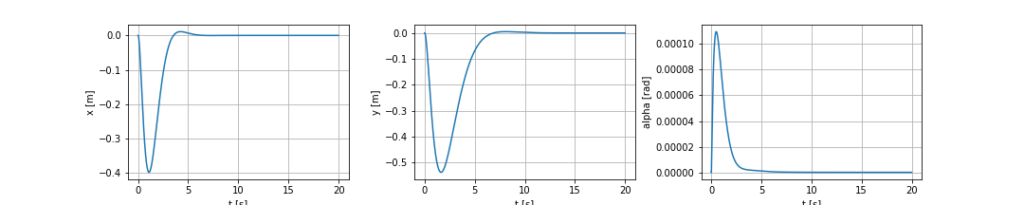
x, y, alpha
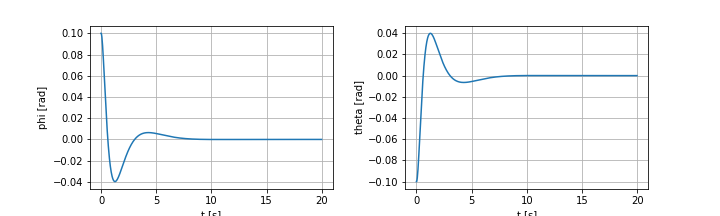
phi, theta
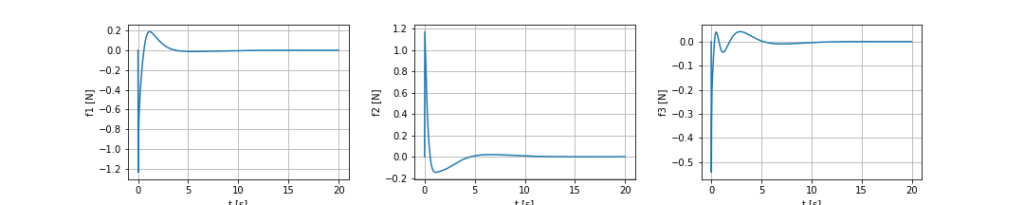
input
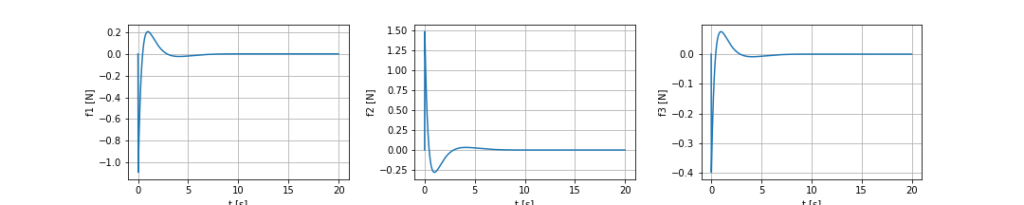
姿勢 $(\phi, \theta) = (0, 0)$ に収束させるために、制御入力 $u$ を変化させていることがわかります。$x, y$ に関しては結構値がぶれていますが $\alpha$ は常に小さいので、機体は振子安定化の際 $x, y$ 軸方向には大きく移動するもののヨー軸周りにはあまり回っていないことがわかります。
描画設定
描画するグラフの設定は以下のように行いました。一行目でグラフのサイズを、二行目でグラフ間の間隔を定めています。figsize はインチ指定のようです。
plt.figure(figsize=(15.0, 3.0))
plt.subplots_adjust(wspace=0.3, hspace=0.6)LQR 制御パラメータの考察(LQR controller parameter consideration)
先程のシミュレーションでは、$Q$ 行列を単位行列、$R$ 行列を単位行列を 10 倍した行列として、これらをもとにリカッチ方程式を解いて制御器を設計しました。この節では、$Q, R$ 行列をそれぞれ変更したときに挙動にどのような違いが出るのかを考察します。
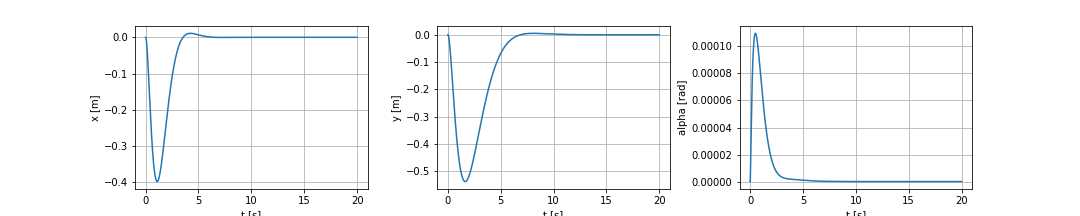
$x$ に重み付けする場合(x weighted case)
$Q$ 行列の $x$ に対応する成分の重みを大きくした場合($Q(1, 1) = 10$)を考えます。このとき、シミュレーション結果は以下のようになります。$Q$ が単位行列のときは $x$ が -0.5 付近まで到達していたのに対し、この制御器では -0.4 程度までしか $x$ は変位しておらず、たしかに $x$ の変位を抑えられていることが伺えます。
$u_2$ に重み付けする場合(u2 weighted case)
$R$ 行列の $u_2$ に対応する成分の重みを大きくした場合($R(2, 2) = 100$)を考えます。このとき、シミュレーション結果は以下のようになります。$R$ が単位行列のときは $u_2$ を 1.5 以上の入力を出していたのに対し、この制御器では 1.2 程度までしか出していません。たしかに $u_2$ の入力を抑えられていることがわかります。
まとめ
今回は、前回の記事で導出したダイナミクスをもとに LQR 制御器を構築し、数値シミュレーションをしてみました。LQR 制御器のパラメータを変更することで挙動が変わることも確認しました。
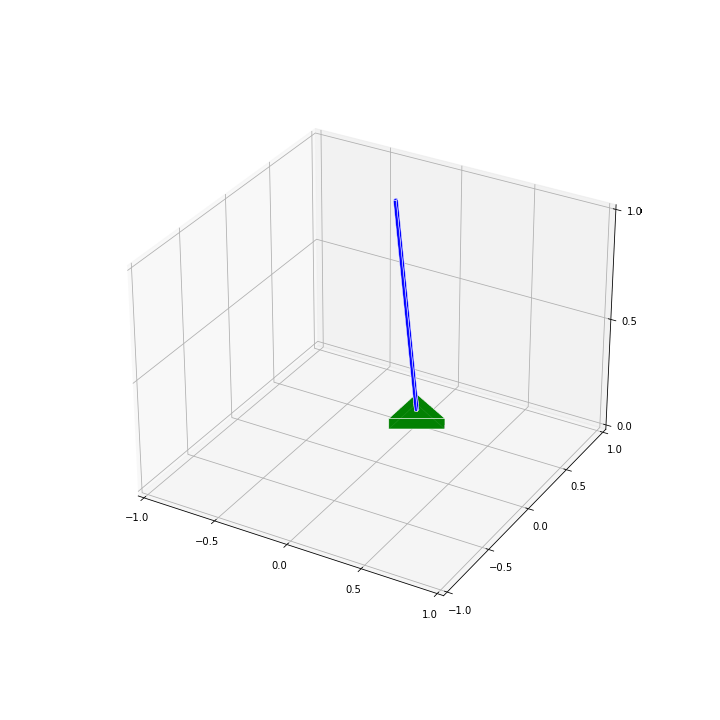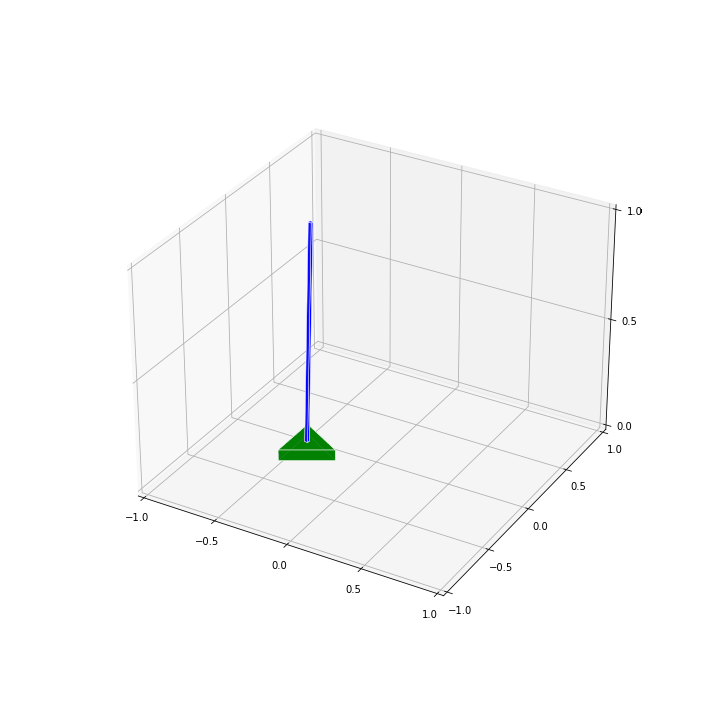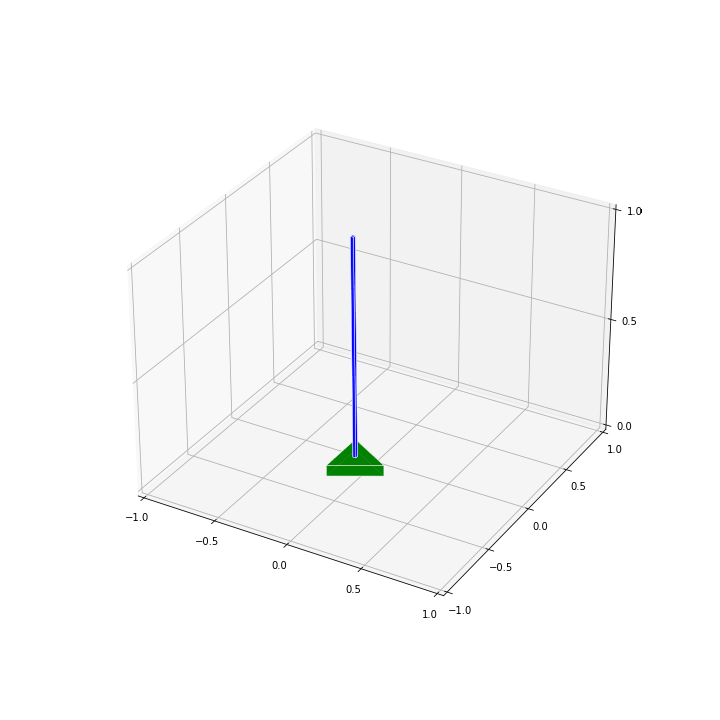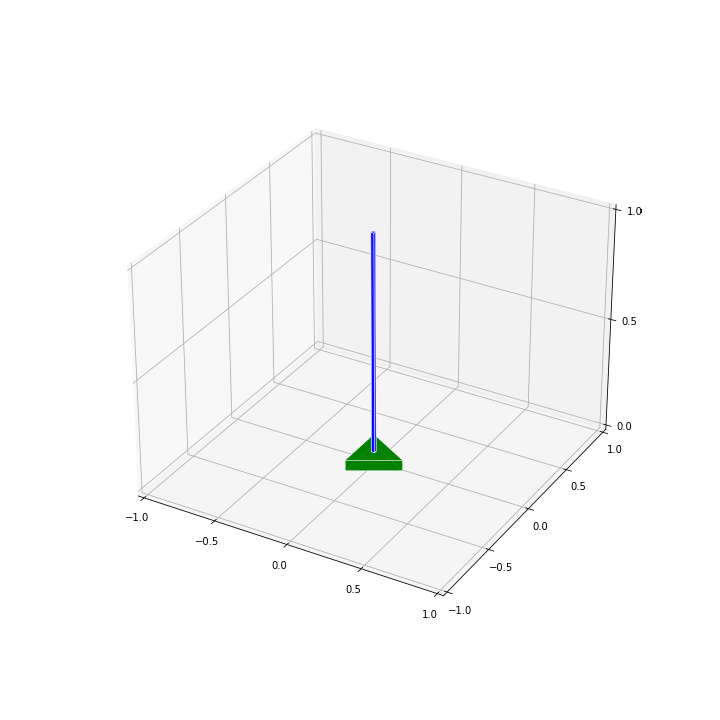
ちなみに、実際にオムニホイールロボットと倒立振子がどのように動くかを下のアニメーションで描画してみました。アニメーションの作成方法についての詳細は、別記事でまとめようと思います。
コメント