オムニホイールロボット上で倒立振子の安定化をしてみたいと思い、本記事を執筆しています。今回は運動方程式の導出とシステムの線形化までです。
背景
大学のときにドローン上での三次元倒立振子の研究をやっていました。以下、当時の動画です。
上の動画の実験では、実験室の天井に計測用カメラを設置する必要あり、個人で実験するのは少しむずかしいなと思うところがありました。しかし、現在は m5stick のような小型で姿勢角を計測できるデバイスもあるので、もしかしたら上記のようなシステムを外部観測機器なしで構築できるのではないかと思っています。
ただ、いきなりドローン + 倒立振子をやってみるというのも危ないので、まずはオムニホイールロボット + 倒立振子で実現可能性を探るというのが今回の試みの趣旨になります。
ちなみに「オムニホイールロボット + 倒立振子」をすでにやっている研究室はありました。↓
概要
今回は運動方程式を導出するため、以下の二つのサイトと論文を参考にしました。
サイト
論文
一つ目のサイトは、簡単な倒立振子モデル(CartPole)を使って、Lagrangian を使った運動方程式の導出方法を説明しています。二つ目のサイトは Kane’s method を使ったドローンの運動方程式導出方法を説明しています。
一つ目のサイトだけだと三次元空間での運動方程式の導出方法がなかなかわからず、二つ目で使われていた Kane’s method はあまりなじみがなかったので、両方のサイトを行ったり来たりしながら運動方程式を導出しました。
システムの定義
以下のようなシステムを考えます。
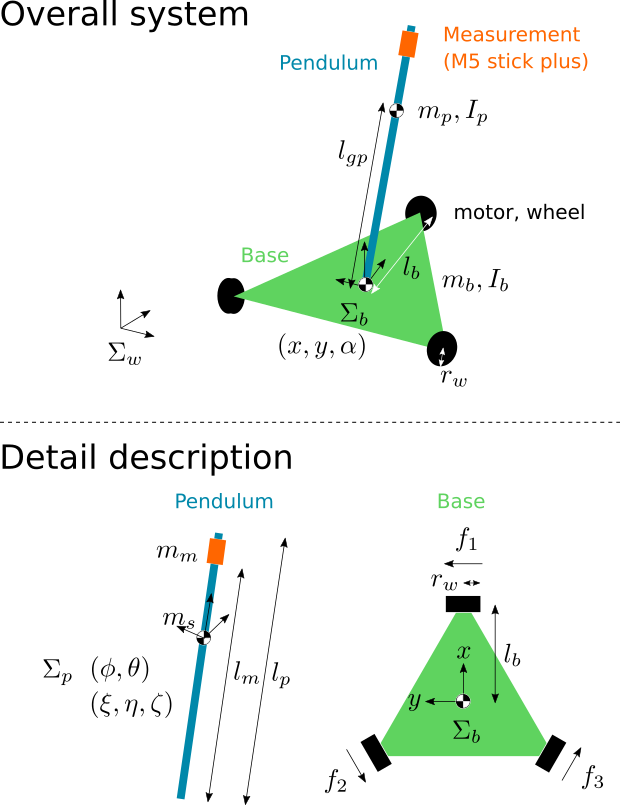
姿勢角の計測に m5stick、振子には 2m 程度の長さのカーボンパイプ、モータはブラシモータ(or サーボモータ?)、車輪はオムニホイール、ロボットの機体は 3D print もしくは CNC 削り出しパーツを使う予定で考えています。
ここらへんは、今後詳細を練っていく予定(12月か来年1月あたりを予定)です。
座標系
| $\Sigma_w$ | ワールド座標系 |
| $\Sigma_b$ | ロボット座標系(原点はオムニホイールロボットの重心) ※添字 b は base の意。 |
| $\Sigma_p$ | 振子座標系(原点は振子の重心) ※添字 p は pendulum の意。 |
状態変数・入力変数
時間微分も含めた状態変数ベクトルは、以下のようになります。
$$ \mathbf{q} = [x, y, \alpha, \phi, \theta, \dot x, \dot y, \dot \alpha, \dot \phi, \dot \theta]^T $$
$$ \mathbf{u} = [f_1, f_2, f_3]^T $$
ロボット
| $x$ | $\mathrm{m}$ | $\Sigma_w$ からみた $x$ 軸方向の $\Sigma_b$ の移動距離($\Sigma_b$ の原点) |
| $y$ | $\mathrm{m}$ | $\Sigma_w$ からみた $y$ 軸方向の $\Sigma_b$ の移動距離($\Sigma_b$ の原点) |
| $\alpha$ | $\mathrm{rad}$ | $\Sigma_w$ からみた $z$ 軸周りの $\Sigma_b$ の回転角 |
振子
| $\phi$ | $\mathrm{rad}$ | 振子の姿勢角 |
| $\theta$ | $\mathrm{rad}$ | 振子の姿勢角 |
振子はワールド座標系 $\Sigma_w$ から見て $x$ 軸周りに $\phi$ 回転し、その結果得られる座標系の $y$ 軸周りにさらに $\theta$ 回転しています。
物理パラメータ
全体
| $g$ | $\mathrm{m/s^2}$ | 重力加速度 |
| $t$ | $\mathrm{s}$ | 時間 |
機体
| $m_b$ | $\mathrm{kg}$ | オムニホイールロボットの重量 |
| $I_b$ | $\mathrm{kg \cdot m^2}$ | 機体の慣性テンソル $\mathrm{diag} \, (I_{bxx}, \, I_{byy}, \, I_{bzz})$ |
| $l_b$ | $\mathrm{m}$ | 機体中心から車輪までの距離 |
| $r_w$ | $\mathrm{m}$ | 車輪半径 |
オムニホイールロボットの場合、ロール軸とピッチ軸周りには傾かないので、$I_{bxx}$ と $I_{byy}$ の値は不要ですが、一応運動方程式導出の際にはこれらの変数も使っています。(導出した運動方程式にこれらの変数は出てきません。)
振子
| $m_p$ | $\mathrm{kg}$ | 振子(棒 + 姿勢角計測用センサ)の重量 |
| $I_p$ | $\mathrm{kg \cdot m^2}$ | 振子の慣性テンソル $\mathrm{diag} \, (I_{pxx}, \, I_{pyy}, \, I_{pzz})$ |
| $l_p$ | $\mathrm{m}$ | 振子の長さ |
物理パラメータに以下も加えようかと考えましたが、今回は簡単のため、振子の重心位置を棒の真ん中 $\frac{l_p}{2}$ とし、さらにセンサも棒の中心位置に置くことにしました。そのため、下記のパラメータは使いません。
- $m_s$:棒の重量
- $m_m$:姿勢角計測用センサの重量
- $l_m$:振子の一端(ロボット側)からの姿勢角計測用センサの距離
- $l_{gp}$:振子の一端(ロボット側)からの振子の重心の距離
このとき、重心周りの振子の慣性テンソルは以下のようになります。$x, \, y$ 軸周りの慣性モーメントを \(\frac{m_p l_p^2}{12}\) として、$z$ 軸周りの慣性モーメントはゼロとしました。(参考サイト)
$$ I_p = \begin{bmatrix} \frac{m_p l_p^2}{12} & 0 & 0 \\ 0 & \frac{m_p l_p^2}{12} & 0 \\ 0 & 0 & 0 \end{bmatrix} $$
モータ
| $f_1$ | $\mathrm N$ | モータ1が出力する力 |
| $f_2$ | $\mathrm N$ | モータ2が出力する力 |
| $f_3$ | $\mathrm N$ | モータ3が出力する力 |
運動方程式と線形近似システムの導出
この節では、運動方程式導出の大まかな流れを解説します。詳しくは github に上がっているソースコードを読んでみてください。
System Description
- 座標の定義
- 物理パラメータの定義(重量・慣性テンソル等)
- 状態変数の定義
- 入力変数の定義
- 状態変数ベクトル $\mathbf q$ の定義
Basic Calculation
- 座標変換
- ワールド座標系からロボット座標系への変換
- ワールド座標系から振子座標系への変換
- ロボット・振子の位置座標と速度の定義(ワールド座標系を基準)
- 3つのモータの位置座標を設定
- ロボットと振子の原点・座標系・質量・慣性テンソルを RigidBody に登録。
- 振子の位置エネルギーを設定。
- 各モータが出力する力を入力として、入力ベクトルを定義。
RigidBody の登録に関しては、このサイトを参考にしました。
Lagrangian
- RigidBody を元に、ワールド座標系でのラグランジアン $L$ を定義。
- 以下の方法で、運動方程式を導出する。 $$ \frac{d}{dt} \frac{\partial L}{\partial \dot q} \ – \ \frac{\partial L}{\partial q} \ = \ F$$
sympy に計算させると、運動方程式の左辺は以下のようになります。右辺は要素がすべてゼロの列ベクトルです。
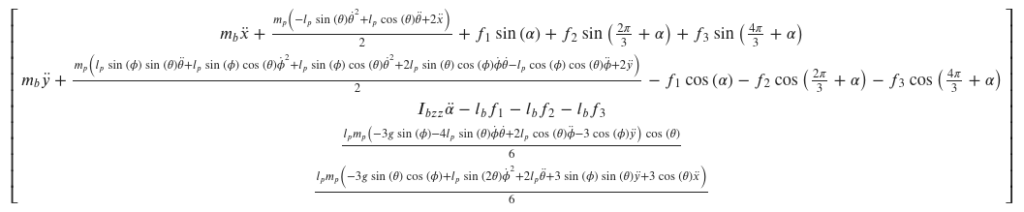
Linearization
- \( [q, \ \dot q]^T \) を状態ベクトルに設定する。(ここでは、$q$ と $\dot q$ を以下としていることに注意。)$$ q \ = \ [x, y, \alpha, \phi, \theta]^T $$ $$ \dot q \ = \ [\dot x, \dot y, \dot \alpha, \dot \phi, \dot \theta]^T $$
- 平衡点を設定する。倒立振子を原点で安定化させたいため、 $$ q \ = \ 0, \ \dot q \ = \ 0$$
- 線形近似したシステムの $A, B$ 行列を求める。
$A, B$ 行列は、以下のようになります。
$$ A = \left[\begin{matrix}0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\0 & 0 & 0 & 0 & \frac{3 g m_{p}}{- 4 m_{b} – m_{p}} & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & \frac{3 g m_{p}}{4 m_{b} + m_{p}} & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & \frac{6 g \left(m_{b} + m_{p}\right)}{l_{p} \left(4 m_{b} + m_{p}\right)} & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & \frac{6 g \left(m_{b} + m_{p}\right)}{l_{p} \left(4 m_{b} + m_{p}\right)} & 0 & 0 & 0 & 0 & 0\end{matrix}\right] $$
$$ B = \left[\begin{matrix}0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0\\0 & \frac{4 \sin{\left(\frac{2 \pi}{3} \right)}}{- 4 m_{b} – m_{p}} & \frac{4 \sin{\left(\frac{4 \pi}{3} \right)}}{- 4 m_{b} – m_{p}}\\\frac{4}{4 m_{b} + m_{p}} & \frac{4 \cos{\left(\frac{2 \pi}{3} \right)}}{4 m_{b} + m_{p}} & \frac{4 \cos{\left(\frac{4 \pi}{3} \right)}}{4 m_{b} + m_{p}}\\\frac{l_{b}}{I_{bzz}} & \frac{l_{b}}{I_{bzz}} & \frac{l_{b}}{I_{bzz}}\\\frac{6}{l_{p} \left(4 m_{b} + m_{p}\right)} & \frac{6 \cos{\left(\frac{2 \pi}{3} \right)}}{l_{p} \left(4 m_{b} + m_{p}\right)} & \frac{6 \cos{\left(\frac{4 \pi}{3} \right)}}{l_{p} \left(4 m_{b} + m_{p}\right)}\\0 & \frac{6 \sin{\left(\frac{2 \pi}{3} \right)}}{l_{p} \left(4 m_{b} + m_{p}\right)} & \frac{6 \sin{\left(\frac{4 \pi}{3} \right)}}{l_{p} \left(4 m_{b} + m_{p}\right)}\end{matrix}\right] $$
$$ \dot{\mathbf{q}} = A \mathbf{q} + B \mathbf{u} $$
エネルギーの検算
この節は、ソースコードだと Verification に対応します。
sympy をはじめて使ったこともあり、RigidBody の使い方が合っているのか等不安だったので、代数学的に運動エネルギーや位置エネルギーを計算した場合と RigidBody を使った場合とで結果が同じになるかどうか確かめてみました。
RigidBodyから算出されるエネルギー
ロボットの運動エネルギー $T_{bk}$ と位置エネルギー $T_{bp}$
display(BodyB.kinetic_energy(Sw).simplify())
display(BodyB.potential_energy.simplify())$$ \displaystyle T_{bk} = \frac{I_{bzz} \dot{\alpha}^{2}}{2} + \frac{m_{b} \left(\dot{x}^{2} + \dot{y}^{2}\right)}{2} $$ $$ \displaystyle T_{bp} = 0 $$
振子の運動エネルギー $T_{pk}$ と位置エネルギー $T_{pp}$
display(BodyP.kinetic_energy(Sw).simplify())
display(BodyP.potential_energy.simplify())$$ T_{pk} = \frac{m_{p} \left(l_{p}^{2} \cos^{2}{\left(\theta \right)} \dot{\phi}^{2} + l_{p}^{2} \dot{\theta}^{2} + 3 l_{p} \sin{\left(\phi \right)} \sin{\left(\theta \right)} \dot{\theta} \dot{y} – 3 l_{p} \cos{\left(\phi \right)} \cos{\left(\theta \right)} \dot{\phi} \dot{y} + 3 l_{p} \cos{\left(\theta \right)} \dot{\theta} \dot{x} + 3 \dot{x}^{2} + 3 \dot{y}^{2}\right)}{6} $$ $$ T_{pp} = \frac{g l_{p} m_{p} \cos{\left(\phi \right)} \cos{\left(\theta \right)}}{2} $$
$T_{bp}$ はロボットの位置エネルギーで、ロボットの重心は基準の高さなので、ゼロになっています。
$T_{bk}$ に関しては、回転による運動エネルギー $\frac{1}{2} I_{bzz} {\dot \alpha}^2$ と並進の運動エネルギー $\frac{1}{2} m_b \left({\dot x}^2 + {\dot y}^2 \right)$ の和なので、正しい式になっています。
問題は $T_{pk}$ と $T_{pp}$ です。下記で、この2つのエネルギーの整合性を確かめていきます。
ちなみに本筋と関係ないですが、長い数式にスクロールバーを表示させる方法はこのサイトを参考にしました。
代数学で求めたエネルギー
振子の位置エネルギー $T_{pp}$
まずは、ロボットの重心から見た振子の重心の位置座標 $[\xi, \eta, \zeta]^T$ を計算します。
振子の重心は、ロボットの重心から距離 \(\frac{1}{2}l_p\) の場所に位置しています。また、振子はワールド座標系 $\Sigma_w$ から見て $x$ 軸周りに $\phi$ 回転し、その結果得られる座標系の $y$ 軸周りにさらに $\theta$ 回転しています。
この座標変換を表す行列 $R_{op}$ は、以下のように表されます。(参考)
$$ R_{op} = R_y (\theta) R_x(\phi) = \left[\begin{matrix}\cos{\left(\theta \right)} & 0 & \sin{\left(\theta \right)}\\\sin{\left(\phi \right)} \sin{\left(\theta \right)} & \cos{\left(\phi \right)} & – \sin{\left(\phi \right)} \cos{\left(\theta \right)}\\- \sin{\left(\theta \right)} \cos{\left(\phi \right)} & \sin{\left(\phi \right)} & \cos{\left(\phi \right)} \cos{\left(\theta \right)}\end{matrix}\right] $$
この行列を元に、以下を計算するとロボット座標系 $\Sigma_b$ から見た振子の重心の位置座標 $[\xi, \eta, \zeta]^T$ が算出されます。
$$ \begin{bmatrix} \xi \\ \eta \\ \zeta \end{bmatrix} = R_{op} \begin{bmatrix} 0 \\ 0 \\ \frac{1}{2} l_p \end{bmatrix} $$
ここで、振子の重心の高さが $\zeta$ と求まったので、$m_p g \zeta$ が振子の位置エネルギー $T_{pp}$ となります。
$$ \zeta = \frac{l_{p} \cos{\left(\phi \right)} \cos{\left(\theta \right)}}{2} $$ $$ T_{pp} = \frac{g l_{p} m_{p} \cos{\left(\phi \right)} \cos{\left(\theta \right)}}{2} $$
これは RigidBody の結果と同じになっていそうですね。
振子の運動エネルギー $T_{pk}$
並進の運動エネルギー $T_{pkt}$ については、以下で導くことができます。
$$ T_{pkt} = \frac{1}{2}( \dot x + \dot \xi )^2 + \frac{1}{2}( \dot y + \dot \eta )^2 + \frac{1}{2}{\dot \zeta}^2$$
回転の運動エネルギー $T_{pkr}$ の導出がちょっと厄介です。このサイトを参考にすると、回転後の座標系 $\Sigma_p$ での角速度ベクトル $\omega_p$ の歪対称行列 $S(\omega_p)$ は以下のように求まります。
$$ S(\omega_p) = R_{op}^T \dot{R_{op}} = \left[\begin{matrix}0 & – \sin{\left(\theta \right)} \dot{\phi} & \dot{\theta}\\\sin{\left(\theta \right)} \dot{\phi} & 0 & – \cos{\left(\theta \right)} \dot{\phi}\\- \dot{\theta} & \cos{\left(\theta \right)} \dot{\phi} & 0\end{matrix}\right] $$
歪対称行列の定義から $\omega_p$ を求めると以下のようになります。
$$ S(\omega) = \begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{bmatrix}$$ $$ \omega_p = \left[\begin{matrix}\cos{\left(\theta \right)} \dot{\phi}\\\dot{\theta}\\\sin{\left(\theta \right)} \dot{\phi}\end{matrix}\right] $$
回転の運動エネルギー $T_{pkr}$ は、振子周りの慣性テンソルを $I_p$ とおいて、以下により求まります。
$$ T_{pkr} = \frac{1}{2} \omega_p^T I_p \omega_p$$
上記の並進と回転の運動エネルギーを加算すると、$T_{pk}$ は以下のようになり、RigidBodyで導出した結果と合致します。
$$ T_{pk} = \frac{m_{p} \left(l_{p}^{2} \cos^{2}{\left(\theta \right)} \dot{\phi}^{2} + l_{p}^{2} \dot{\theta}^{2} + 3 l_{p} \sin{\left(\phi \right)} \sin{\left(\theta \right)} \dot{\theta} \dot{y} – 3 l_{p} \cos{\left(\phi \right)} \cos{\left(\theta \right)} \dot{\phi} \dot{y} + 3 l_{p} \cos{\left(\theta \right)} \dot{\theta} \dot{x} + 3 \dot{x}^{2} + 3 \dot{y}^{2}\right)}{6} $$
これらにより、RigidBody で求めても代数学的に求めても力学的エネルギーはすべて合致したことになります。
ソースコード
ソースコードは以下の github に載せています。上記の節でそれぞれの処理の内容について説明しているので、本節では説明を省きます。
トラブルシューティング
sympy の display() 関数
sympy の display() 関数で、以下のような warning が出ました。
~/.local/lib/python3.8/site-packages/IPython/lib/latextools.py:126: MatplotlibDeprecationWarning: The to_png function was deprecated in Matplotlib 3.4 and will be removed two minor releases later. Use mathtext.math_to_image instead.
latextools.py というファイルの126行目があやしそうだったので、ここを以下のように変更したら warning は出なくなりました。
- mt.to_png(f, s, fontsize=12, dpi=dpi, color=color)
+ mathtext.math_to_image(s, f, dpi=dpi)まとめ
今回は、今作りたいと思っている「オムニホイールロボット + 倒立振子」のシステムの概要を述べ、運動方程式の導出・線形化等を行いました。
次回の記事で数値シミュレーションまでできたらと思っています。
コメント