AtCoder Beginner Contest 185: E – Sequence Matchingの初心者解説（二次元DP）

Software

この問題は難しかったです．いくつかの解説サイトを見ないと理解できませんでした．やっぱりDP（動的計画法）は難しいですね．

問題

公式の問題はこちらです．

問題文

長さ $N$ の整数列 $A$ と長さ $M$ の整数列 $B$ があります．$A$ と $B$ に以下の操作を行います．

  • $A$ と $B$ のそれぞれからいくつかの要素を取り除き、残った要素をそのままの順番でつなげて新たな整数列 $A’$ と $B’$ を作る．
  • この際，一つも要素を取り除かなくても，全部取り除いても構わない．
  • $A$ と $B$ は同じ長さになるようにする．

$A, B$ から取り除いた合計要素数を $x$ とし，$A’_i ≠ B’_i$ を満たす $i$ の数を $y$ とするとき，スコア $x + y$ の最小値を求めてください．

制約

  • $1 ≦ N, M ≦ 1000$
  • $1 ≦ A_i, B_i ≦ 10^9$
  • 入力は全て整数

解説

公式の解説，けんちょんさんの解説を見ると，この問題はDPで解くのが正攻法みたいです．

DP時のテーブルの作り方について，この記事が非常に詳しかったので参考にしました．

大枠は，部分整数列（並び替えはしない）を抽出して，DPで逐次的にスコアを求めていき，最終的に $A, B$ のスコアを割り出していくという方針です．

この問題は，数式だけを示しても理解に苦しむと思うので，以下の例ではどうなるかを補足説明しながら解説していきます．

例）
$A = [1, 2, 1, 3]$
$B = [1, 3, 1]$

DP配列との添字の混乱を避けるため，配列 A[i], B[j] はそれぞれ A[1], B[1] から値を格納していくこととします．たとえば，例では，A[1] = 1, A[2] = 2 です．

ここで，配列 dp[i][j] を以下のように定義します．

dp[i][j] := $A$ の 1〜i までの部分整数列と $B$ の 1〜j までの部分整数列のスコア．ただし，i = 0 のときは $A$ は何も要素を含まない空集合とし，j = 0 のときは $B$ が空集合であるとする．

後の説明のため，以下を定義します．

  • $A[1:i]$ := $A$ の 1〜i までの部分整数列
  • $B[1:j]$ := $B$ の 1〜j までの部分整数列

たとえば例題だと，dp[3][2] は，$A[1:j] = [1, 2, 1]$ と $B[1:j] = [1, 3]$ という整数列を考えたときのスコアということになります．

ここで，dp[i][j] の更新規則を以下のように定めます．

初期条件

  • dp[0][0] を $0$ とする．これは，両方とも空集合の場合を考えると自明．
  • dp[i][j] (i≠0, j≠0) を INT_MAX とする．

更新手順

  • ①：$A$ の i までの部分整数列 $A[1:i]$ の末尾を削除した場合のスコアを考える．
    • ①のスコア：dp[i-1][j] + 1
  • ②：$B$ の j までの部分整数列 $B[1:j]$ の末尾を削除した場合のスコアを考える．
    • ②のスコア：dp[i][j-1] + 1
  • ③：$A[1:i]$ と $B[1:j]$ の末尾を比較する．
    • $A[1:i]$ と $B[1:j]$ の末尾が同一の場合
      • ③のスコア：dp[i-1][j-1]
    • $A[1:i]$ と $B[1:j]$ の末尾が異なる場合
      • ③のスコア：dp[i-1][j-1] + 1
  • ①〜③のスコアの中で最小のものを，dp[i][j]（$A[1:i], B[1:j]$ のスコア）とする．

抽出できる部分整数列（並び替えはしない）を考えて，DPで逐次的にスコアを求めていくと最終的に $A, B$ のスコアを割り出せるということです．

例題の最終的なテーブルは以下のようになり，答えは $2$ となります．

B\A01234
001234
110123
221122
332212

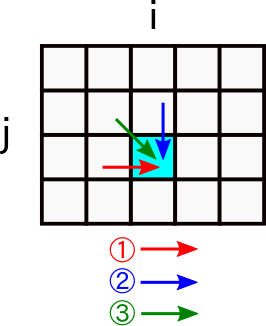
テーブルは以下のように，左・上・斜め左上の要素から更新されます．これを繰り返して，テーブルが完成します．左の要素からの更新は更新手順①に対応します．同様に，上の要素からの更新は更新手順②に，斜め左上の要素からの更新は更新手順③に対応します．

ソースコード

#include <bits/stdc++.h>
using namespace std;

void chmin(int &a, int b) { if(a>b) a=b; }

int main(void) {
    int N, M;
    cin >> N >> M;
    vector<int> A(N+1, 0);
    vector<int> B(M+1, 0);
    vector<vector<int>> dp(N+1, vector<int>(M+1, INT_MAX));
    for (int i=1; i<=N; i++) { cin >> A[i]; }
    for (int i=1; i<=M; i++) { cin >> B[i]; }

    dp[0][0] = 0;
    for (int i=0; i<=N; i++) {
        for (int j=0; j<=M; j++) {
            if (i>0) {
                // delete the last element of A.
                chmin(dp[i][j], dp[i-1][j] + 1);
            }

            if (j>0) {
                // delete the last element of B.
                chmin(dp[i][j], dp[i][j-1] + 1);
            }

            if (i>0 && j>0)  {
                // compare the last elements of A and B (true is 1, false is 0.).
                chmin(dp[i][j], dp[i-1][j-1] + !(A[i]==B[j])); 
            }
        }
    }

    cout << dp[N][M] << endl;

    return 0;
}

chmin という関数を定義しました．第一引数と第二引数を比較して，第二引数の方が小さければ第一引数に第二引数を代入するという内容の関数です．

まとめ

二次元DPに関して学びました．例題を考え，テーブルの更新方法を図示したので，少しDPについて理解を深められたかと思っています．

ただ，DPに関しては慣れが必要かもしれませんね…．

コメント