AtCoder Beginner Contest 185: D – Stampの初心者解説（ソート・切り上げ・境界条件）

Software
2020.12.26

問題

公式の問題はこちらです．

問題文

$N$ 個のマスが並んでいます．左から $i$ 番目のマスをマス $i$ と呼ぶことにします．この $N$ 個のマスのうち、マス $A_1$， マス $A_2$，マス $A_3$，…，マス $A_M$ の $M$ 個のマスは青色で，それ以外のマスは白色です．ただし，$M = 0$ の場合，青色のマスはありません．

正整数 $k$ を一つ選んで幅 $k$ のハンコを作ります．幅 $k$ のハンコを使用して，連続する白色の $k$ マスを選び，それらを赤色に塗り替えることを考えます．このとき， $k$ 個のマスの中に青色のマスが入っていてはなりません．

$k$ とハンコの使用方法をうまく決めた時，最小で何回ハンコを使用すれば，白色のマスが存在しない状態にすることができるでしょうか．

制約

  • $1 ≦ N ≦10 ^9$
  • $0 ≦ M ≦ 2 \times 10^5$
  • $1 ≦ A_i ≦ N$
  • $A_i$ は互いに異なる
  • 入力は全て整数

解説

以下の図のように，白色のマスを赤色に変えることを考えます．

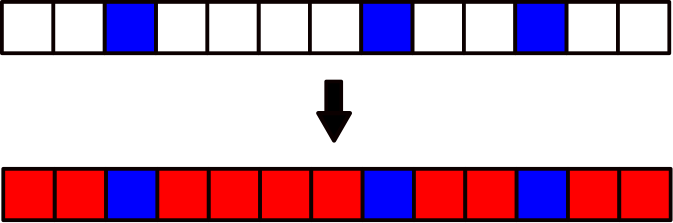
連結している白のマスの数の最小値をハンコの大きさ $k$ とし，この $k$ の大きさのハンコで白いマスを赤くしていきます．上記例だと，連結している白のマスの数は $2$ と $4$ であり，最小値は $2$ なのでハンコの大きさ $k$ は $2$ となります．なおこの際，ハンコの大きさが $0$ というのはありえないので，$k ≧ 1$ になることに注意します．

白いマスを赤くする際にハンコを押す回数は，「連結している白のマスの数をハンコの大きさで割ってから切り上げ，これらの総和を取る」ことで求まります．切り上げる操作に関しては，割り切れないときに重ねてハンコを押さなければならないため必要です．たとえば連結している白のマスの数が $3$ でハンコの大きさが $2$ だったときに，ハンコは $2$ 回押さないとダメですね．

ざっくりプログラムの処理の流れを書くと，以下のようになります．入力される青のマスの位置は昇順（小さい順）で並べられているわけではないので，計算の処理を簡単化するためにソートするのがポイントです．

  1. 青色のマスの位置を A[i] に格納する．
  2. A[i] をソートする．
  3. 青のマスがなければ，ハンコの大きさは $N$ とする．
  4. 青のマスがあれば，白のマスの連結数を逐次求め，その最小値をハンコの大きさ $k$ とする．
  5. 最後に，白のマスの連結数をハンコの大きさ $k$ で割って切り上げ，これらの総和を取ることで，ハンコを押す回数を求める．

C++だとソートする関数はデフォルトであるんですね．めちゃ便利です．ソートの平均計算量は $O (M \log M)$ になります．ソートしていれば，連結している白のマス数を A[i] - A[i-1] - 1 のように簡単に計算することができます．

このサイトを参考にすると，割って切り上げるのは結構簡単で，割られる数を $a$，割る数を $b$ とすると，以下のように求まります．

$$ (a + b – 1) / b$$

また，このような問題では境界条件についても考えることが非常に重要です．

  • 全部のマスが白の場合
  • 全部のマスが青の場合

前者は，ハンコの大きさを $N$ とすることで，通常時と同様に計算できます．後者は，ハンコを押す必要がありませんね．この場合，上記のアルゴリズムの5で，白のマスの連結数がすべて $0$ となるので，計算結果は期待通り $0$ となります．

ソースコード

以下で AC 取れました！

#include <bits/stdc++.h>
using namespace std;

int main(void) {
    int N, M;
    cin >> N >> M;
    vector<int> A(M);          // there are M areas with blue stamps.
    vector<int> Adiff(M+1);    // there are M+1 areas with white stamps.
    for (int i=0; i<M; i++) cin >> A[i];
    sort(A.begin(), A.end());

    int k = INT_MAX;
    for (int i=0; i<=M; i++) {
        if (M==0) { Adiff[0] = N; k = N; break; } // the case there is no blue stamps.

        int tmpdiff = 0;
        if (i==M) { tmpdiff = N - A[M-1]; }       // right end
        else if (i==0) { tmpdiff = A[0] - 1; }    // left end
        else { tmpdiff = A[i] - A[i-1] - 1; }
        Adiff[i] = tmpdiff;
        if (k > tmpdiff && tmpdiff > 0) { k = tmpdiff; }
    }

    int ans = 0;
    for (int i=0; i<=M; i++) {
        ans += (int) (Adiff[i] + (k - 1)) / k; // round up
    }
    cout << ans << endl;

    return 0;
}

感想

この問題は結構簡単な部類に入るのではないかと思いました．境界条件を考えるのが少し面倒だったかもしれません．

コメント