AtCoder Beginner Contest 185: C – Duodecim Ferraの初心者解説（オーバーフロー注意）

Software
2020.12.26

Duodecimはラテン語で 12 という意味らしいです．Ferraはたぶん鉄のことを表していそうです．鉄の棒を12分割する問題なので，このような名前なのかと思います．

この問題はオーバーフローに気をつけないと解けません．オーバーフローに関しては，このサイトがかなりわかりやすく説明してくれていました．

問題

公式の問題はこちらです．

問題文

長さ $L$ の鉄の棒が東西方向に横たわっています．この棒を 11 箇所で切断して，12 本に分割します．このとき分割後の各棒の長さが全て正整数になるように分割しなければなりません．分割のパターンが何通りあるかを求めてください．
なお，この問題の制約下で答えは $2^{63}$ 未満であることが証明できます．

制約

  • $ 12 ≦ L ≦ 200 $
  • $L$ は整数

解説

解いてみる

問題文だけ見ると結構簡単そうな問題ですね．たとえば，以下のような長さ 15 の棒を考えると，長さ 1 ごとに区切った 14 本の点線のうち，どの線を選んで分割するかで分割のパターンが変わってきます．たとえば，赤線のように区切った場合がパターンのうちの一つです．

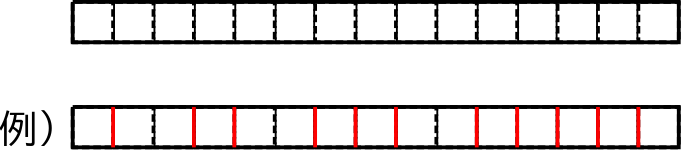
$L = 15$ の場合は 14 本の点線から 11 本を選べば良いので，$_{14}C_{11}$ 通りの分割のパターンがあることになり，これを計算すれば答えが求まります．

すなわち，一般化して長さ $L$ の棒を考えたとき，分割のパターンは $_{L-1}C_{11}$ であり，この計算結果が答えとなります．$_{L-1}C_{11}$ は以下のように計算できます．

$$ \frac{(L-1) \times (L-2) \times … \times (L-11)}{11 \times 10 \times … \times 1} $$

では，上記を踏まえてソースコードにしてみます．

#include <iostream>
using namespace std;

int main (void) {
    long long L = 0;
    cin >> L;

    long long ans = 0;
    long long ele = 11*10*9*8*7*6*5*4*3*2;
    ans = (L-1) * (L-2) * (L-3) * (L-4) * (L-5) * (L-6) * (L-7) * (L-8) * (L-9) * (L-10) * (L-11) / ele;
    cout << ans << endl;

    return 0;
}

これで良さそうに見えますが，このソースコードだとオーバーフローしてしまって WA になってしまいます．次節でオーバーフローについて考えます．

オーバーフローについて考える

オーバーフローについては冒頭で紹介した下記のサイトがとてもわかりやすいので，詳しくはこちらを参照していただきたいですが，本記事でも軽くまとめます．

データ型の範囲について記載されているこのサイトを参照すると，long long型は以下の範囲を取れます．

-9,223,372,036,854,775,808 から 9,223,372,036,854,775,807

ちょっと数が大きすぎてあまりイメージできないかもしれませんが，例えば9,223,372,036,854,775,808はlong long型では表現できないわけですね．

#include <iostream>
using namespace std;

int main(void) {
    long long a;
    a = 9223372036854775808;
    cout << a << endl;

    return 0;
}

ためしに上記のコードを実行すると，実行結果は以下のようになります．

-9223372036854775808

オーバーフローして，変数 a の格納結果がlong long型の最小値となってしまっています．このようにデータの範囲から桁あふれして正常に数値を表現できないことをプログラミングの世界でオーバーフローといいます．

オーバーフロー対策

問題に戻って考えてみます．先のコードを実行し，たとえば $L = 199$ としてみると，実行結果は-77838502262となります．分割パターンが負の数になるのは明らかにおかしいのでオーバーフローしていることがわかると思います．

何故オーバフローしてしまうのかというと，今回の問題では分子が大きくなりすぎるからです．

$$ \frac{(L-1) \times (L-2) \times … \times (L-11)}{11 \times 10 \times … \times 1} $$

これは，以下のように変形することができます．

$$ \frac{L-1}{1} \times \frac{L-2}{2} \times \frac{L-3}{3} \times … \times \frac{L-11}{11} $$

コードで表すと以下のようになります．

long long ans = 1;
for (int i=1; i<=11; i++) {
    ans *= L-i;
    ans /= i;
}

このように都度割っていくことで，long long型の変数 ans に格納する値を小さくしています．整数にならないのでは？と不安に思うかもしれませんが，for文の中での ans の途中計算結果は $_{L-i}C_{i}$ となるため，常に整数になります．（$i$ は for 文のイテレータに対応します．）たとえば $i=3$ では下記のようになります．

$$ _{L-3}C_{3} = \frac{L-1}{1} \times \frac{L-2}{2} \times \frac{L-3}{3} $$

全体のソースコードは以下のようになります．これで AC 通りました！

#include <iostream>
using namespace std;

int main (void) {
    long long L = 0;
    cin >> L;

    long long ans = 1;
    for (int i=1; i<=11; i++) {
        ans *= L-i;
        ans /= i;
    }
    cout << ans << endl;

    return 0;
}

ちなみに，問題文の「答えは $2^{63}$ 未満である」というのはlong long型の変数で処理可能な範囲だよと教えてくれていますね．long long型は 8 byte = 64 bit で，$2^{64}$ 通りの変数を格納でき，$-2^{63}$ 以上 $2^{63}$ 未満の整数となります．

感想

オーバーフローについて説明できるレベルでなかったのでまとめておきました．オーバーフローは組込みエンジニアにも必須の知識ですね！

コメント