問題
公式の問題はこちらです.
問題文
縦 $H$ マス,横 $W$ マスの 2 次元グリッドで表された街があります.上から $i$ 行目,左から $j$ 列目のマスの情報が文字 $a_{i, j}$ により与えられます.$a_{i,j}$ は S , G , . , # , a ~ z のいずれかです.# は入ることができないマスを,a ~ z はテレポーターのあるマスを表します.
S のマスからスタートして,以下のいずれかの移動により G のマスまで移動します.このときの最短の手数を求めてください.どうしても G のマスにたどり着けない場合は,代わりに -1 を出力してください.
- 現在いるマスと上下左右に隣り合う,# でないマスに移動する.
- 今いるマスと同じ文字が書かれているマスを 1 つ選び,そこにテレポートする.この移動は現在いるマスが a ~ z のいずれかであるとき使える.
制約
- 1 ≤ $H,W$ ≤ 2000
- $a_{i,j}$ は S , G , . , # , 英小文字のいずれか
- S のマスと G のマスはちょうど 1 つずつ存在する
解説
公式の解説はこちらです.
概要
テレポータがなければ,幅優先探索という手法で解けるみたいです.さらに,テレポータがあるマップ上で幅優先探索をすると計算量が膨大になってしまうため,計算にひと工夫加えます.
ひと工夫に関しては後の節でもう少し詳しくまとめようと思いますが,簡単にはテレポータに最初に到達したときのみ他のテレポータへの移動を考え,2回目以降にテレポータに到達したときは他のテレポータへの移動は考えないという工夫です.
幅優先探索
そもそも幅優先探索とは何でしょう?
以下の記事が,迷路のアニメーションを使って幅優先探索と深さ優先探索の違いを説明していて非常にわかりやすかったです.

グラフ理論を用いて幅優先探索を詳細に説明している以下の記事を見ると,より理解が深まると思います.深さ優先探索はスタック,幅優先探索はキューを使って実装できるみたいです.

深さ優先探索と幅優先探索の違いを簡潔に説明すると以下のようになります.
- 深さ優先探索(DFS):ある状態からはじめ,状態遷移ができなくなるまで状態を進め,遷移ができなくなったら1つ前の状態に戻る.この試行を繰り返して探索する.
- 幅優先探索(BFS):はじめの状態に近い方から順番に探索する.
先程も紹介したこの記事の動画のコンセプトをお借りして図解します.以下のような,左上の S がスタートのマス,右下の G がゴールのマスである 3 x 3 の迷路を想定します.
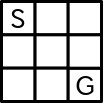
幅優先探索では,1ステップでたどり着ける場所,2ステップでたどり着ける場所…と順番に探索していき,そこにゴールがあるかを判定します.下図ではステップごとに色分けをしてあります.薄い色から濃い色に行くにしたがって,ステップ数が増えていきます.

この図から,4ステップ目でゴールにたどり着くことがわかると思います.このように幅優先探索でスタートからゴールまでの最小ステップ数(最短経路)を求めることができます.近い場所からゴールを探していってゴールを見つけたら探索終了ということですね.
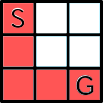
他にもいくつか経路はありますが,最短経路は例えば以下のようになりますね.
計算量を抑えるひと工夫
計算量の求め方の概要
計算量を求める方法については,以下の記事がシンプルでわかりやすかったです.

for (int i = 0; i < n; i++) {
count++; // n回実行
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
count++; // n^2回実行
count++; // n^2回実行
}
}上のコードは $O(n^2)$ の計算量となります.実際には $2n^2 + n$ 回の計算が行われますが,最高次の項以外の項と係数を除くことで, 計算量は $O(n^2)$ と書き表されます.
テレポータがない場合の計算量
問題の解説に戻ります.a -z のテレポータが存在しない場合を考えると,たとえば以下のようなマップとなります.
S...... ....... ....... ......G
この場合,$HW$ のマスでたかだか4方向(上下左右)にしか動けないので,探索回数は $4HW$ となり,計算量は $O(HW)$ となります.
※実際には,S の位置では壁があるため上と左には動けないという制約や訪れたことのあるマスには移動しないという制約を加えるため,$4HW$ よりも探索回数は少なくなります.
テレポータがある場合の計算量
ここでは,テレポータがあることにより計算量が大きくなってしまう場合を考えます.たとえば以下のマップは極端な例ですが,かなり計算量が増えてしまいます.
Saaaaaa aaaaaaa aaaaaaa aaaaaaG
この場合,移動できるテレポータは S, G, 自分 を除いて $HW – 3$ あります.つまり,移動できるマスの種類は $HW – 3$ になります.この極端なマップでは,$HW – 3$ の中に上下左右の動きも含まれているので +4 は加えません.
これを踏まえて探索回数を求めると $(HW – 2)(HW – 3) + 2$ となり,計算量は $O(H^2W^2)$ となります.
S, G を除く $HW – 2$ 個のマスから $HW – 3$ の場所に移動でき,S から「右,下」の2方向に移動できるため,探索回数は上記のようになります.
計算量を少なくするひと工夫
ここでやっと,ひと工夫の話になります.ここまでの話が大分長かったですね.
おさらいすると,テレポータに最初に到達したときのみ他のテレポータへの移動を考え,2回目以降にテレポータに到達したときはテレポータ間移動は考えないというのが今回のひと工夫です.
たとえば,以下のようなマップを思い浮かべるとイメージしやすいかもしれません.3つテレポータがありますが,テレポータ間移動は最初に赤太字のテレポータaに到達したときのみを考えれば十分です.
S...a.. .a..... .....a. ......G
上の例だと,「S → . → 赤太字のa → 青太字のa → . → G」という経路が最短ですね.たとえば緑太字のaから青太字のaにテレポートした場合は,最短経路より明らかに遅いです.
「二回目以降にテレポータに到達してからテレポータ間移動をした場合」は,「最初にテレポータに到達してからテレポータ間移動をする場合」よりも早くゴールに到達することはありません.こういうの数学的に証明したいですね….
ここで,先程の大量の「a」のテレポータがある以下のマップを再度用いて,計算量を再度計算してみます.
Saaaaaa
aaaaaaa
aaaaaaa
aaaaaaG
はじめてテレポータ a に到達したときは,自分・S・Gを除く $HW – 3$ 個の移動の選択肢があり,テレポート後の $HW – 4$ 個のマスではたかだか4つしか移動の選択肢がありません.
テレポート後のマスでは,テレポートはもう使えないはずなので,「a」を「.」に読み替えます.厳密には,スタート位置の違う $HW – 4$ 個のマップができます.テレポート後は,たとえば以下のマップに読み替えることができるということです.(右下の a にテレポートした場合)
##..... ....... ......S ......G
先と同様に S の位置では移動方向の選択肢が2つあります.これらを踏まえると,探索回数は
$$ 2 + (HW – 3) + 4(HW – 4) = 5HW – 17$$
以下となり,計算量は $O(HW)$ となります.
※今回は G 付近にテレポートできるマップだったので,上記の探索回数となりましたが,他のマップだともう少し探索回数は増えそうですね.
キュー(queue)とスタック(stack)について
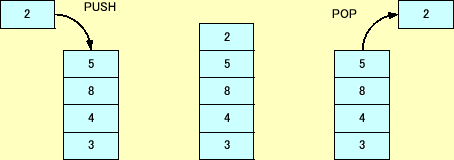
軽くまとめると,キューがFIFO(First In First Out)でスタックが(Last In First Out)です.このサイトのイメージ図が簡潔でわかりやすいです.
キューのイメージは以下です.
http://www.yamamo10.jp/yamamoto/lecture/2005/2E/test_4/html/node2.html
スタックのイメージは以下です.
http://www.yamamo10.jp/yamamoto/lecture/2005/2E/test_4/html/node2.html
キューの使い方はこのサイトが参考になります.
ソースコード
さて,実装をしようとするとやっぱりわかりません….こういう問題は慣れが必要そうですね.
けんちょんさんのソースコードと蟻本を見ながら書いてみました.
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> P;
// define moving directions. ex: (dx[1], dy[1]) = (0, +1)
vector<int> dx = {1, 0, -1, 0};
vector<int> dy = {0, 1, 0, -1};
int main(void) {
// input variables from user
int H, W; // maze size
scanf("%d %d", &H, &W);
vector<string> maze(H);
for (int i=0; i<H; i++) { cin >> maze[i]; }
// (x, y) coordinates of start and goal
int sx, sy, gx, gy;
// alphabets position (a - z)
vector<vector<P>> apos(26);
// search start, goal and alphabet position
for (int i=0; i<H; i++) {
for (int j=0; j<W; j++) {
if ( maze[i][j]=='S' ) { sx = i; sy= j; }
if ( maze[i][j]=='G' ) { gx = i; gy= j; }
if ( maze[i][j] >= 'a' && maze[i][j] <= 'z' ) {
apos[maze[i][j] - 'a'].push_back(P(i,j));
}
}
}
bool used[26];
memset(used, false, sizeof(used));
vector<vector<int>> dist(H, vector<int>(W, -1));
dist[sx][sy] = 0;
queue<P> q;
q.push(P(sx, sy));
while (!q.empty()) {
P p = q.front();
q.pop();
int x = p.first;
int y = p.second;
if (maze[x][y] >= 'a' && maze[x][y] <= 'z') {
int c = maze[x][y] - 'a';
if (used[c] != true) {
for (auto tmp:apos[c]) {
if (dist[tmp.first][tmp.second] == -1) {
q.push(tmp);
dist[tmp.first][tmp.second] = dist[x][y] + 1;
}
}
used[c] = true;
}
}
for (int i=0; i<4; i++) {
int nx = x + dx[i]; // x coodinate of next step
int ny = y + dy[i]; // y coodinate of next step
if (nx >= 0 && nx < H && ny >= 0 && ny < W && maze[nx][ny]!='#' && dist[nx][ny]==-1) {
q.push(P(nx, ny));
dist[nx][ny] = dist[x][y] + 1;
}
}
}
cout << dist[gx][gy] << endl;
return 0;
}全体の流れ
細かいところはソースコードを見ていただきたいので,全体のソースコードの流れだけ列挙しておきます.
- マップのサイズを定義する.
- スタート・ゴール・a-zがある位置を探索して,変数に格納する.
- 以下を定義する.
- used[i]: すでにテレポートしたアルファベットかどうかを表す配列
- dist[x][y]: スタートからの (x, y) 座標のマンハッタン距離
- q: 探索用キュー
- 最短経路探索
- 他のテレポータへの移動を考える.(最初にそのテレポータに到達したときのみ)
- 上下左右4方向への移動を考える.(マップ外・#・すでに探索したマスへの移動は考えない.)
- 最短路を表示.
詰まったところ
マップの定義
vector<string> maze(H);
for (int i=0; i<H; i++) { cin >> maze[i]; }
マップは,一次元の string 型の vector として定義します.例として,以下のようなマップが入力のときは maze[0] に S.b.b が入り,maze[1] に a.a.G が入ります.要素としては,maze[0][0] に “S”,maze[0][1] に “.” が入っています.
S.b.b a.a.G
はじめ,二次元配列 string[][] を作ろうと思いましたが,セグフォやコンパイルエラーが出ました.二次元配列を new で作るのは結構大変みたいなので,vector を使ったほうが良いですね.
また,このサイトによると,二次元配列でかなり大きな領域を確保しようとするとセグフォしてしまうみたいです.maze[2001][2001] の配列を作ろうとしたときセグフォしました.
a -zの位置をリスト化する
if ( maze[i][j] >= 'a' && maze[i][j] <= 'z' ) {
apos[maze[i][j] - 'a'].push_back(P(i,j));
}
マップの i 行目 j 列目にある文字を maze[i][j] としたとき,この文字が a – z の間のアルファベットかどうかは上記の if 文で判定できます.
maze[i][j] が 0x61(ASCIIコードで ‘a’ は 0x61)以上で,0x7a(ASCIIコードで ‘z’ は 0x7a)以下のとき,上記の if 文が trueになります.このとき apos という vector の要素に座標を追加します.たとえば,apos[0] には a の座標のリストが,apos[1] には b の座標のリストが格納されています.
ここでは,ASCIIコードで文字同士を比較しているということです.ちなみに,ASCIIコード表はこちらのサイトにあります.
テレポートするごとに最短路が +1 余分に足されるバグ
※これは備忘録です.
if (dist[tmp.first][tmp.second] == -1) {
q.push(tmp);
dist[tmp.first][tmp.second] = dist[x][y] + 1;
}
上記コードの if 文を最初書いておらず,すでに到達しているか未到達に関わらず,最短路に +1 していました.これにより,テレポートごとに余分に最短路が +1 されるというバグが発生していました.
その他
Cっぽい書き方とC++っぽい書き方
↓こちらがCっぽい書き方
bool used[26]; memset(used, false, sizeof(used));
↓こちらがC++っぽい書き方
vector<bool> used(26, false);
どちらも長さ26の配列(vector)を作って false で埋める処理をしていますが,C++っぽい書き方の方が短く書けますね.これからは後者の書き方をしていきたいと思います.
配列の中身を参照するときはどちらの場合でも,used[1] のようにすればよいです.つまり使い方も同じです.
まとめ
幅優先探索とキューの使い方,計算量を下げる方法を学びました.



コメント