AtCoder Beginner Contest 184: D – increment of coinsの初心者解説（確率DP, メモ化再帰）

Software
2020.12.08

問題

公式の問題はこちらです．

問題文

袋の中に金貨が A 枚，銀貨が B 枚，銅貨が C 枚入っています．袋の中にあるいずれかの種類の硬貨が 100 枚になるまで，袋の中の硬貨をランダムに 1 枚増やします．操作回数の期待値を求めてください．

制約

  • 0≤A,B,C≤99
  • A+B+C≥1

解説

公式の解説はこちらです．あと，毎度けんちょんさんの記事がわかりやすいです．

概要

そもそも期待値の定義ってなんだろう？というところから調べてみると，以下が定義のようです．

期待値とは、1回の試行で得られる値の平均値のことで、得られうるすべての値とそれが起こる確率の積を足し合わせたものです。

https://bellcurve.jp/statistics/course/6349.html

操作回数の期待値はいずれかのコインが100枚のときに0となります．いずれかのコインが100枚のとき，もうコインを引く操作が必要ない（操作回数が+0）ためです．

また，金貨・銀貨・銅貨がそれぞれ $a, b, c$ 枚あるときの操作回数の期待値を $f(a, b, c)$ とすると，金貨が出たときの操作回数の期待値は以下のようになります．

$$\frac{a}{a+b+c} (f(a+1,b,c)+1)$$

上記のように，金貨が出る確率と金貨が出た場合の見込みの試行回数を掛け合わせれば，金貨が出たときの操作回数の期待値が割り出せます．分解すると以下のようになります．

  • $\frac{a}{a+b+c}$：金貨が出る確率
  • $f(a+1, b, c)$：金貨・銀貨・銅貨がそれぞれ $a+1, b, c$ 枚のときの操作回数の期待値
  • +1は金貨を引いたときに足される操作回数

はじめ公式解説を見たとき $f(a+1, b, c)$ の期待値に操作回数（+1）を加えて確率をかけるという操作がイマイチピンと来ませんでしたが，期待値の定義から $f(a+1, b, c)$ はコインがそれぞれ $(a+1, b, c)$ 枚あるときの操作回数の平均値を表していると考えると納得できました．

金貨・銀貨・銅貨それぞれが引かれる可能性があることを踏まえると，$f(a,b,c)$ を以下のように書き換えることができます．以下の式のように漸化式風に書き直すことができ，さらにいずれかのコインが100枚のときに操作回数の期待値は0になるので，再帰的に操作回数の期待値を求めることができます．

$f(a, b, c) = \frac{a}{a+b+c} (f(a+1, b, c) + 1) + \frac{b}{a+b+c} (f(a, b+1, c) + 1) + \frac{c}{a+b+c} (f(a, b, c+1 + 1))$

メモ化再帰

この問題は確率DP（ダイナミックプログラミング・動的計画法）と呼ばれる問題の一種だそうで，これを実装する手法としてメモ化再帰という手法を使うのが良いそうです．DPに関しては，以下のサイトを参考にしました．

上記記事の中で，ナップザック問題に関する解説がありましたが，あまり理解できなかったので改めて別のタイミングで勉強しようと思います (^^;;

さて，話を戻すと，今回やりたいことは金貨・銀貨・銅貨いずれかのコインが100枚のときの操作回数0を基準とし，再帰を使って操作回数の期待値を割り出していくことです．このとき，毎回期待値を計算していると非常に膨大な計算量になってしまいます．

というのも，たとえば金貨・銀貨・銅貨が98枚ずつのケースを考えたとき，再帰の呼び出し図は以下のようになります．f(98, 98, 98) は f(99, 98, 98) と f(98, 99, 98) と f(98, 98, 99) を呼び出し，f(99, 98, 98) は f(100, 98, 98) と…を呼び出すといった形で操作回数を求めていきます．

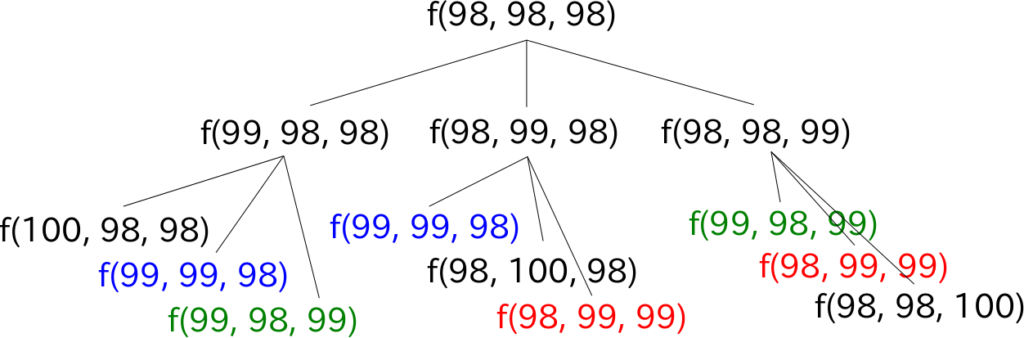
上図を見ると，呼び出す値が重複しています．黒以外の同色で示されている箇所が呼び出す値が重複している部分です．これでもまだ呼び出し図の一部ですが，3組重複していることがわかります．初期の枚数がもっと少なければ相当な回数重複した計算が発生することがわかりますね…．

このように，複数回呼び出されてしまう（複数回計算されてしまう）値が存在しているわけです．

そこで，メモ化という技術を使います．dp[101][101][101] のサイズの配列を持っておき，一度計算した値はここに答えを格納しておきます．たとえば，金貨・銀貨・銅貨がそれぞれ 10, 10, 10 枚あるときの操作回数の期待値は dp[10][10][10] の要素に格納します．同じ枚数の組の期待値を計算しようとした場合，保存しておいた配列の値をリターンします．

コードを一部抜粋すると以下のような形です．

double calc_exval(int a, int b, int c) {
    if (dp[a][b][c] >= 0) { return dp[a][b][c]; };

ソースコード

#include <stdio.h>
#include <string.h>

double dp[101][101][101];

// exval stands for expected values
double calc_exval(int a, int b, int c) {
    if (dp[a][b][c] >= 0) { return dp[a][b][c]; };
    if (a==100 || b==100 || c==100) { return 0; }
    double e = 0;
    e += (double)a/(a+b+c) * (calc_exval(a+1, b, c) + 1);
    e += (double)b/(a+b+c) * (calc_exval(a, b+1, c) + 1);
    e += (double)c/(a+b+c) * (calc_exval(a, b, c+1) + 1);
    dp[a][b][c] = e;

    return e;
}

int main(void) {
    int A, B, C;
    scanf("%d %d %d", &A, &B, &C);

    memset(dp, -1, sizeof(dp));
    double e = calc_exval(A, B, C); 
    printf("%f\n", e);

    return 0;
}

memset関数を使うためにstring.hが必要だったのでインクルードしました．最初にmemsetでdp配列の各要素を-1で初期化しておいて，dp[a][b][c] に値が入っていればその値を返すというメモ化再帰をしました．

以下の部分をコメントアウトしてメモ化再帰を使わずに，たとえば金貨・銀貨・銅貨をそれぞれ0, 0, 1枚とすると計算は終わりません笑．

if (dp[a][b][c] >= 0) { return dp[a][b][c]; };

感想

確率は高校数学でもめちゃくちゃ苦手だったので，理解するのにかなり時間がかかりました…．あと，自分でも解説がうまく言語化できていないように思えてます（泣）．ココがわかりにくい等のコメントあれば遠慮なくお願いします．

コメント