AtCoder Beginner Contest 184: C – Super Ryumaの初心者解説

Software
2020.11.23

AtCoder初心者でまだ灰色コーダーですが，調子に乗って解説記事を書いてみます(@.@;;)

昨日のAtCoderのC問題Super Ryumaがわからなすぎて落ち込んでいたのですが，ネットの情報を見る限りこの問題かなり難しかったようですね．少し安心しました．

解説ページを読んでも理解するのに苦しんだので，僕と同じような方がいらっしゃるかもしれないと思い解説記事の解説記事を書いてみています．初心者だからこそ上級者が端折っちゃう解説ポイントも踏まえられたらよいなと思っています．もし何かご指摘あれば遠慮なくお願いします．

問題

問題の詳細は，公式をご覧ください．

問題文

無限に広がる 2 次元グリッドがあり，マス (r1, c1) に駒「超竜馬」が置かれています．この駒はマス (a, b) にあるとき，以下のいずれかの条件を満たすマス (c, d) に動かすことができます．

  • a+b = c+d
  • a-b = c-d
  • |a-c| + |b-d| <= 3

超竜馬を (r1, c1) から (r2, c2) に動かすのに必要な最小手数を求めてください．

超竜馬が動けるマスは以下のようなイメージです．

https://atcoder.jp/contests/abc184/tasks/abc184_c

制約

  • 入力は全て整数
  • 1 <= r1, c1, r2, c2 <= 10^9

解説

公式の解説ページはここです．他にも解説しているサイトは以下のようなものがありました．これらのサイトを参考にさせていただいています．

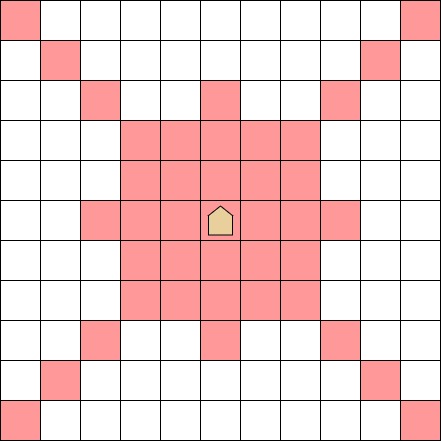
超竜馬は任意のマスに3手以内移動できる

大前提として，超竜馬は任意のマスに3手以内移動できるそうです．解いている最中は，これがわからず再帰的に探索する方法ばかり考えていました．

超竜馬が3手で任意のマスに移動できる理由のは超竜馬が以下の動きをできるからです．これら2種類の移動を組み合わせれば多くても3手で任意のマスに到達することができます．

  • 3番目の法則（|a-c| + |b-d| <= 3）により，超竜馬は1手で上下左右の隣り合うマスいずれかに移動できる
  • 以下の図で任意の同じ色のマス目に，2手で移動できる．

https://atcoder.jp/contests/abc184/editorial/339

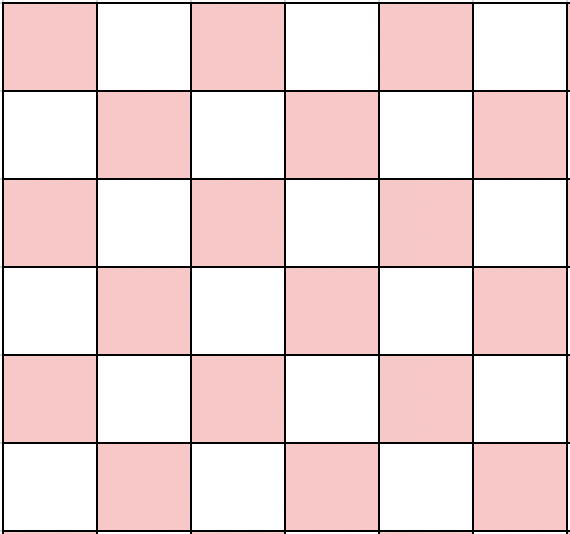
上記の2つ目がなかなかピンと来ないかもしれませんが，1番目の法則（a+b = c+d）と2番目の法則（a-b = c-d）によって，超竜馬は下記のように将棋の角のような動きをできるため，2手で同じ色のマス目にいけるいうわけです．

  • 1番目の法則は，(b-d)/(a-c) = -1 と変形することができ，傾きが-1で (a, b) を通る直線上の任意のマスに移動できる（下図の赤色の移動に対応．）
  • 2番目の法則は，(b-d)/(a-c) = 1 と変形することができ，傾きが1で (a, b) を通る直線上の任意のマスに移動できる（下図の青色の移動に対応．）

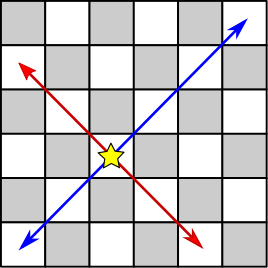
こうなると，3手未満で目標のマスに到達できるかどうかをそれぞれの手数で判定し，いずれにも当てはまらなければ移動に3手かかるとみなせば良さそうです．0手で到達できなければ1手で到達できないか，1手で到達できなければ2手で到達できないかを判定していきます．

0手で (r2, c2) に到達する場合

これは簡単ですね．(r1, c1) = (r2, c2) の場合です．

1手で (r2, c2) に到達する場合

以下の条件を満たすときに，1手で (r2, c2) に到達できます．これもc++であればabs()を使えば簡単に実装できると思います．

  • r1+c1 = r2+c2
  • r1-c1 = r2-c2
  • |r1-r2| + |c1-c2| <= 3

ちなみに，この3つ目の条件は (r1, c1) と (r2, c2) のマンハッタン距離が3以内というらしいです．マンハッタン距離についてはこのサイトが詳しいですが，「座標軸に平行にしか移動できない条件下での到達するまでに必要なマス数」と捉えるとわかりやすいかと思います．

たとえば以下の赤星から青星までのマンハッタン距離は5です．

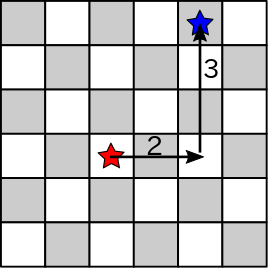
2手で (r2, c2) に到達する場合

難しいのはここですね．公式解説と同様，便宜上問題文の3つの移動方法をそれぞれ，A, B, Cと名付けます．

移動方法条件式
Aa+b = c+d
Ba-b = c-d
C|a-c| + |b-d| <= 3

(r1, c1) -> (r2, c2) に2手で移動する場合は，A->B, C->C, A->C, B->Cの4つの移動方法があります．他の移動方法については以下の理由で考慮不要です．

  • A->A, B->B: これらは1手で移動できてしまう．
  • B->A, C->A, C->B: 「Aの移動の後にBの移動をしたときの到着地点」と「Bの移動の後にAの移動をしたときの到着地点」は同じ．（ベクトルの足し算は可換．）

A->Bの移動について

A->Bの移動は，下記の図の同じ色のマスに移動することと同義です．

https://atcoder.jp/contests/abc184/editorial/339

これは，以下の条件に書き直すことができます．イメージ図も載せておきます．

  • (r1, c1) と (r2, c2) のマンハッタン距離が偶数

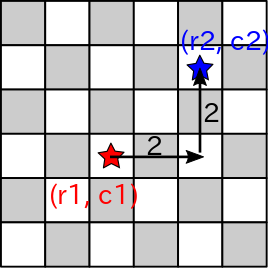
C->Cの移動について

マンハッタン距離が6以下となればよいです．条件は以下です．

  • | r1 – c1 | + | r2 – c2 | <= 6

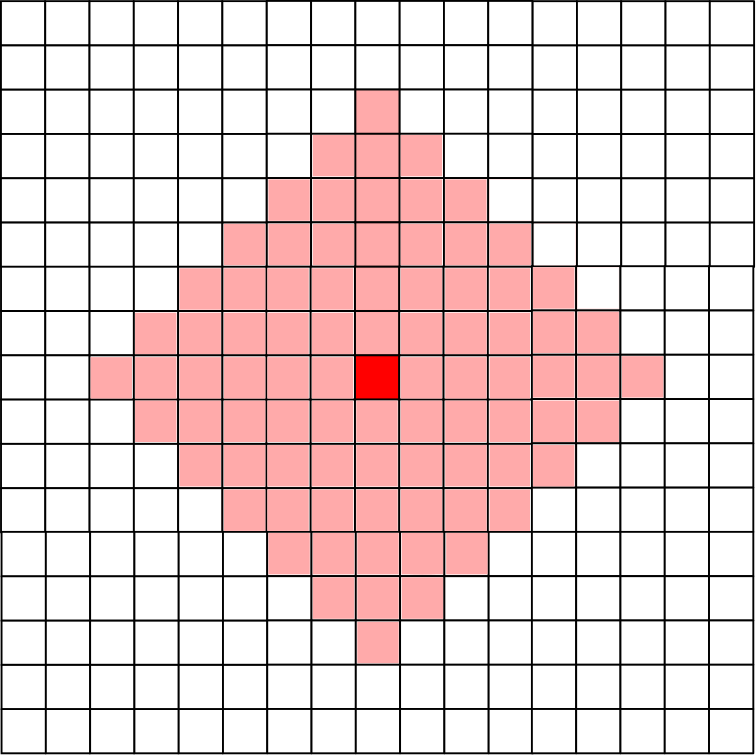
※濃い赤が移動前地点 (r1, c1) です．以降も同様です．

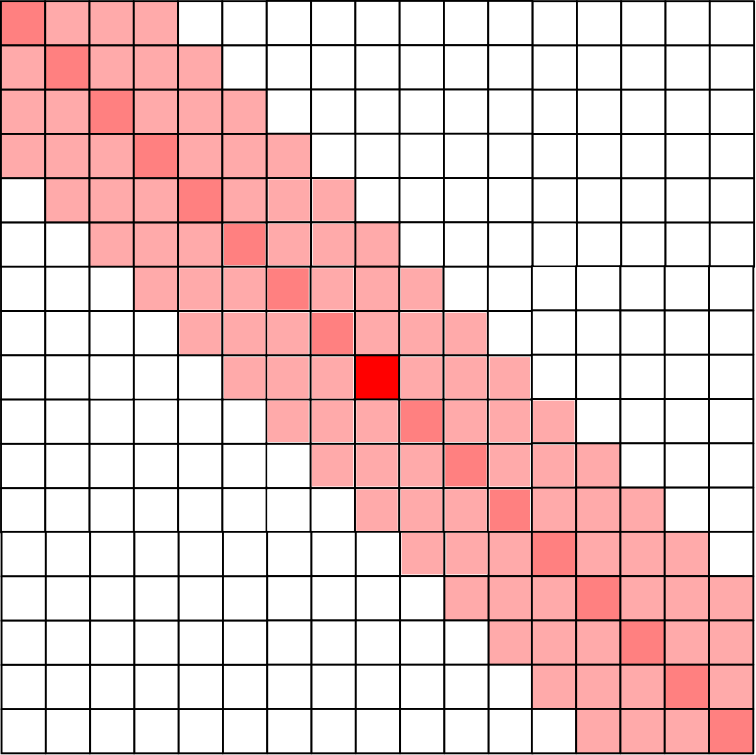
A->Cの移動について

Aの移動で，以下の条件を満たす場所に移動します．（下図の濃いピンク）

  • r1+c1 – (r2 + c2) = 0

ここからさらに，Cの移動をした後の場所は以下の条件式で表される場所となります．（下図の淡いピンク）

  • | r1 + c1 – (r2 + c2) | <= 3

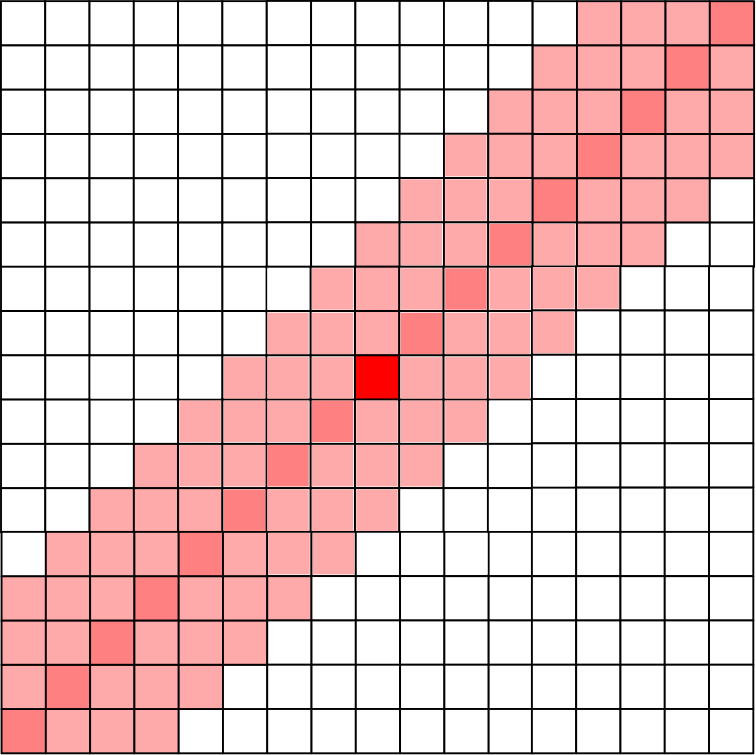
B->Cの移動について

A->Cの移動と同様に，条件式は以下です．

  • | r1 – c1 – (r2 – c2) | <= 3

ソースコード

以下のコードでACになりました！！

#include <stdio.h>
#include <iostream>

using namespace std;

int main(void) {
    int r1, c1, r2, c2;
    scanf("%d %d", &r1, &c1);
    scanf("%d %d", &r2, &c2);

    int ans = 0;
    if (r1==r2 && c1==c2) { ans = 0; }
    else if ((r1+c1==r2+c2) || (r1-c1==r2-c2) || (abs(r1-r2)+abs(c1-c2)<=3) ) { ans = 1; }
    else if (((abs(r1-r2)+abs(c1-c2))%2==0) || abs(r1-c1)+abs(r2-c2)<=6 || abs(r1+c1 - r2-c2)<=3 || abs(r1-c1 - r2+c2)<=3) { ans = 2; }
    else { ans = 3;}

    printf("%d\n", ans);

    return 0;
}

感想

やっぱりこの問題難しいですね．似たような問題が出されたら制限時間以内に解ける気がしないです…マンハッタン距離等初めて知る概念もあったので，勉強になりました．

コメント